Read the following chapters in The Practice of Statistics

• 2003: pgs 450-451
• 2012: pg 324

When the space shuttle Challenger exploded shortly after lift off, it was the responsibility of the investigation team to find the cause of this tragedy. Their findings assigned the cause of the explosion to the "O-rings" whose function was to contain the rocket fuel within the fuel cells. When the rocket fuel leaked outside the fuel cell, it was ignited by the exhaust and the subsequent explosion followed.

Bayes' theorem is used in this type of problem solving. Given an event in the present, a probability is found linking the present event to an event in the past (its probable cause).

"This is Bayes' Theorem. It is named after Rev. Thomas Bayes, an 18th century mathematician who derived a special case of this theorem. Bayes' calculations were published in 1763, two years after his death. Exactly what Bayes intended to do with the calculation, if anything, still remains a mystery today. However, this theorem, as generalized by Laplace, is the basic starting point for inference problems using probability theory as logic."

Bayes' Theorem

Where: B is the given present event and A₁, A₂, ..., A_k are events in the past.

In the previous lesson, Contingency Tables, the P(Person taking a Claritin-D capsule and experiencing a headache) was 0.1086. Using Bayes' Theorem find the conditional probability: P(Took Claritin-D | Experienced a headache)

The tree diagram from the previous section will prove helpful in solving this problem.

Using Bayes' Theorem

Thus P(Took Claritin-D | Experienced a headache) is about 57.6%

Bayes' Theorem, Simplied (Based on a Tree Diagram)

Where: B is the given present event A₁ is an event in the past.

Example 1: Using the tree diagram and the simplified Bayes' Theorem, find P(Took Claritan-D | Experienced a Headache)

Solution:

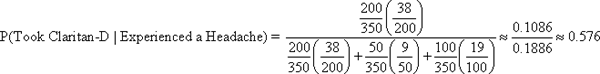
Thus P(Took Claritan-D | Experienced a Headache) is about 57.6%.

Example 2: A manufacturer of DVD players has two suppliers for their microchips. Supplier 1 provides 75% of their microchips and the remainder are provided by Supplier 2. Supplier 1 has a 2.5% defective rate and Supplier 2 has a 3.8% defective rate. A defective microchip is found, what is the probability it came from Supplier 2? Find P(Supplier 2 | Defective microchip).

Solution: Use a tree diagram and Bayes' Theorem to solve this problem. The tree diagram is:

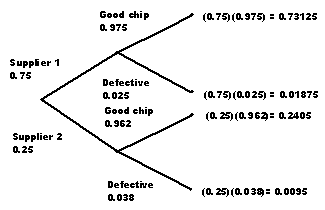
Bayes' Theorem is:

Thus there is a 33.6% chance the defective microchip was provided by Supplier 2.

Use the following website if you need additional help.

• Bayes' Theorem