9.05 Area and Volume of Irregular Shapes

Try It

Surface Area Practice

Problem #1

1. Find the total surface area of the following shape.
   

   

   
   
   • How many faces does this shape have?

     Answer: 12

   
   
   • What is the total surface area?

     Answer: 538
     
     How to Solve:
     
     (12)(8) = 96
     (3)(7) = 21
     (12)(8) = 96
     (3)(7) = 21
     (12)(7) = 84
     (3)(4) = 12
     (4)(7) = 28
     (3)(4) = 12
     (8)(7) = 56
     (4)(7) = 28
     (8)(7) = 56
     (4)(7) = 28
     

Problem #2

2. Find the total surface area of the following shape.
   

   

   
   
   • How many faces does this shape have?

     Answer: 10

   
   
   • What is the total surface area?

     Answer: 1,440
     
     How to Solve:
     
     Front and back: 2[(21)(21) – (9)(9)] = 720
     Outside faces: 4[(6)(21)] = 504
     Inside faces: 4[(6)(9)] = 216
     720 + 504 + 216 = 1,440

Problem #3

3. Find the total surface area of the following shape.
   

   

   
   
   • How many faces does this shape have?

     Answer: 8

   
   
   • What is the total surface area?

     Answer: 750
     
     How to Solve:
     
     Outside faces:
     (15)(7) = 105
     (11)(7) = 77
     (13)(7) = 91
     (9)(7) = 62
     (4)(7) = 28
     (4)(7) = 28
     Front and back:
     [(13)(11) + (9)(4)] = 358
     
     105 + 77 + 91 + 62 + 28 + 28 + 358 = 750

Problem #4

4. Find the total surface area of the following shape.
   

   

   
   
   • How many faces does this shape have?

     Answer: 5

   
   
   • What is the total surface area?

     Answer: 1,886
     
     How to Solve:
     
     A = ½ bh
     A = ½ (22) 16
     A = 176
     A = ½ bh
     A = ½ (22)(16)
     A = 176
     A = lw
     A = (26)(18) = 468
     A = lw
     A = (26)(22) = 572
     A = lw
     A = (26)(19) = 494
     176 + 176 + 468 + 572 + 494 = 1,886

Problem #5

5. Find the total surface area of the following shape.
   

   

   
   
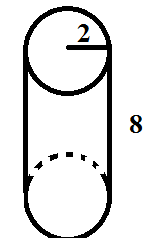
   • What formula should you use?

     Answer:SA = 2πr² + πdh

   
   
   • What is the total surface area?

     Answer:40π
     
     How to Solve:
     
     SA = 2πr² + πdh
     SA = 2π(2²) + π(4)(8)
     SA = 2π(4) + π(4)(8)
     SA = 8π + 32π
     SA = 40π

Problem #6

6. Find the total surface area of the following shape.
   

   

   
   
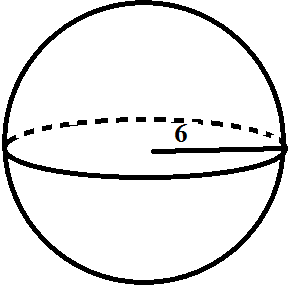
   • What formula should you use?

     Answer: SA = 4πr²

   
   
   • What is the total surface area?

     Answer: 144π
     
     How to Solve:
     
     SA = 4πr²
     SA = 4π(6²)
     SA = 4π(36)
     SA = 144π

Problem #7

7. Find the total surface area of the following shape.
   

   

   
   
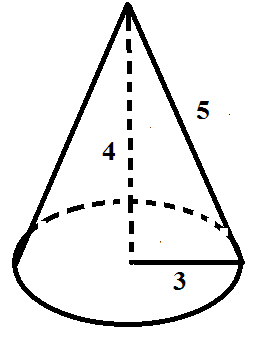
   • What formula should you use?

     Answer: SA = πr² + πrl

   
   
   • What is the total surface area?

     Answer: 24π
     
     How to Solve:
     
     SA = πr² + πrl
     SA = π(3²) + π(3)(5)
     SA = π(9) + π(15)
     SA = 24π

Volume Practice

Problem #8

8. Find the volume of the following shape.
   

   

   
   
   • How many rectangular prisms is this divided into?

     Answer: 2

   
   
   • What is the volume?

     Answer: 756
     
     How to Solve:
     
     V = lwh
     V = (7)(8)(12)
     V = 672
     V = lwh
     V = (3)(4)(7)
     V = 84
     672 + 84 = 756

Problem #9

9. Find the volume of the following shape.
   

   

   
   
   • How many rectangular prisms should you divide this into?
     
     Hint
     
     

     Answer: 4

   
   
   • What is the total volume?

     Answer: 2,160
     
     How to Solve:
     
     2[(6)(21)(6)] = 1,512
     2[(6)(9)(6)] = 648
     1,512 + 648 = 2,160

   
   
   • There is another way to solve this problem.

     Answer: You can also find the volume of the entire shape and then subtract the piece cut out of the center.
     
     V = lwh
     V = (21)(21)(6)
     V = 2,646
     
     V = lwh
     V = (9)(9)(6)
     V = 486
     2,646 − 486 = 2,160

Problem #10

10. Find the volume of the following shape.
    

    

    
    
    • How many rectangular prisms should you divide this into?
      
      Hint
      
      

      Answer: 2

    
    
    • What is the volume?

      Answer: 1,253
      
      How to Solve:
      
      V = lwh
      V = (15)(9)(7)
      V = 945
      V = lwh
      V = (4)(11)(7)
      V = 308
      945 + 308 = 1,253

    
    
    • There is another way to solve this problem.

      Answer: You can also find the total volume and subtract the piece that is missing from the corner.
      
      V = lwh
      V = (15)(13)(7)
      V = 1,365
      
      V = lwh
      V = (4)(4)(7)
      V = 112
      1,365 − 112 = 1,253

Problem #11

11. Find the volume of the following shape.
    

    

    
    
    • What formula should you use?

      Answer: V = πr²h

    
    
    • What is the volume?

      Answer: 32π
      
      How to Solve:
      
      V = πr²h
      V = π(2²)(8)
      V = π(4)(8)
      V = 32π

Problem #12

12. Find the volume of the following shape.
    

    

    
    
    • What formula should you use?

      Answer: V = 4/3 πr³

    
    
    • What is the volume?

      Answer: 288π
      
      How to Solve:
      
      V = 4/3 πr³
      V = 4/3 π(6³
      V = 4/3 π(216)
      V = 288π

Problem #13

13. Find the volume of the following shape.
    

    

    
    
    • What formula should you use?

      Answer: V = 1/3 πr²h

    
    
    • What is the volume?

      Answer: 12π
      
      How to Solve:
      
      V = 1/3 πr²h
      V = 1/3 π(3²)(4)
      V = 1/3 π(9)(4)
      V = 1/3 π(36)
      V = 12π