9.05 Area and Volume of Irregular Shapes

Learn

Area of Irregular Shapes

To find the area of irregular shapes, the first thing to do is to divide the irregular shape into regular shapes that you can recognize such as triangles, rectangles, circles, and squares.

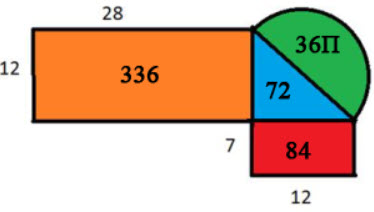
We can divide the irregular shape above into regular shapes, shown below.

Then, you find the area of each of these shapes and add them together. On this particular shape below, you will have to use the Pythagorean Theorem to find the diameter of the semi-circle.

Find the areas of the regular shapes:

1. Find the area of the orange rectangle:
   
   • A = lw
   • A = 12(28) 
   • A = 336


2. Find the area of the blue triangle:
   
   • A = ½ bh
   • A = ½ (12)(12)
   • A = 72


3. Find the area of the red rectangle:
   
   • A = lw
   • A = 12(7)
   • A = 84


4. Use Pythagorean Theorem to find the diameter of the semi-circle:
   
   • a² + b² = c²
   • 12² + 12² = c²
   • 144 + 144 = c²
   • 288 = c²
   • √288 = √c²
   • 12√2 = c


5. Remember to half the diameter to get the radius and find the area of the green semi-circle:
   
   • A = ½ π r²
   • A = ½ π (6√2)²
   • A = 36π


6. Add all of the areas together to find the area of the irregular shape:
   
   • 336 + 72 + 84 + 36π = ____
   • 492 + 36π

See how each of the irregular shapes make up the overall irregular shape and how the different areas can be combined.

Surface Area of Irregular Shapes

On this shape we are going to calculate the surface area. The surface area is the sum of the area of all of the faces.

Before we begin, we must determine how many faces there are.

How many faces do you think this shape has?

Answer: The shape has 8 faces.

It may help to make a net of this shape when determining faces. A net is a flattened out three dimensional solid.

Imagine you cut enough edges of the shape below so that it would lay flat. The net image here is an example of what you end up with.

Find the surface area of each part of the net.

1. Find the area of the red rectangle:
   
   • A = lw
   • A = 3(16) 
   • A = 48


2. Find the area of the orange rectangle:
   
   • A = lw
   • A = 3(13) 
   • A = 39


3. Find the area of the dark green rectangle:
   
   • A = lw
   • A = 3(20)
   • A = 60


4. Find the area of the purple square:
   
   • A = lw
   • A = 3(3)
   • A = 9


5. Find the area of the light green rectangle:
   
   • A = lw
   • A = 3(17)
   • A = 51


6. Find the area of the blue square:
   
   • A = lw
   • A = 3(3)
   • A = 9

The gold faces are a little different from the others. We do not have a formula for this shape so you will need to divide it into smaller shapes that we do have a formulas for.

Divide each shape into two rectangles. To find the area of each shape, you will have to find the area of each rectangle and add them together.

Shape A:

1. Find the area of the first rectangle:
   
   • A = lw
   • A = 3(16)
   • A = 48


2. Find the area of the second rectangle:
   
   • A = lw
   • A = 3(13)
   • A = 39


3. Add the first and second triangle together for the total area:
• Total Area = 48 + 39
• Total Area = 87

Shape B:

1. Find the area of the light green rectangle:
   
   • A = lw
   • A = 3(16)
   • A = 48


2. Find the area of the blue square:
   
   • A = lw
   • A = 3(13)
   • A = 39


3. Add the first and second triangle together for the total area:
• Total Area = 48 + 39
• Total Area = 87

Add all of the areas together to get the total surface area:

48 + 39 + 60 + 9 + 51 + 9 + 87 +87 = 390

The total surface area of the three dimensional shape is 390.

Surface Area of a Cylinder

Let's find the surface area of the cylinder below.

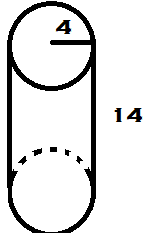
You will use the following formula to solve for the surface area: SA = 2πr² + πdh

You will notice that the top and bottom are circles so part of the formula is 2 times the area of a circle. If you were to slice the rest of the cylinder open, it would be in the shape of a rectangle so part of your formula is for the area of a rectangle (lw) except we have to find the length by finding the circumference of the circle.

1. Fill in all of the information you know into the formula.
   SA = 2πr² + πdh
   
   SA = 2π(4²) + π(8)(14)



2. Simplify the problem. It is acceptable to leave your answer in terms of pi unless you are told to do something else.
   SA = 2π(4²) + π(8)(14)
   
   SA = 32π + 112π
   
   SA = 144π

The surface area of this cylinder is 144π.

Surface Area of a Sphere

Let's find the surface area of the sphere below.

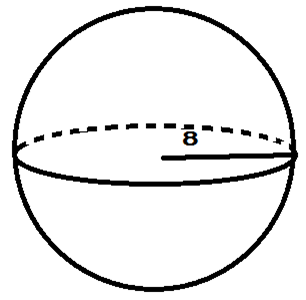
You will use the following formula to solve for the surface area: SA = 4πr²

1. Fill in all of the information you know into the formula.
   SA = 4πr²
   
   SA = 4π(8²)



2. Simplify the problem. It is acceptable to leave your answer in terms of pi unless you are told to do something else.
   SA = 4π(8²)
   
   SA = 4π(64)
   
   SA = 256π

The surface area of this sphere is 256π.

Surface Area of a Cone

Let's find the surface area of the cone below.

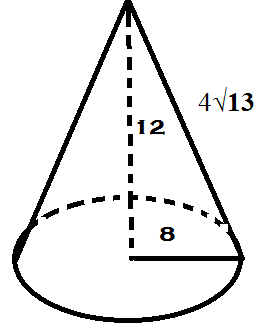
You will use the following formula to solve for the surface area: SA = πr² + πrl

The first part of the formula finds the area of the base. In the second part of the equation, the l is for the slant height, which is 4√13 in this instance.

1. Fill in all of the information you know into the formula.
   SA = πr² + πrl
   
   SA = π(8²) + π(8)(4√13)



2. Simplify the problem. It is acceptable to leave your answer in terms of pi unless you are told to do something else.
   SA = π(8²) + π(8)(4√13)
   
   SA = 64π + 32√13π

The surface area of this cone is 64π + 32√13π.

Volume of Irregular Shapes

We can also find the volume of irregular shapes.

Our first step is to separate the shape into separate rectangular prisms.

1. Find the volume of the blue rectangular prism.
   
   • V = lwh
   • V = (6)(3)(17)
   • V = 306


2. Find the volume of the pink rectangular prism.
   
   • V = lwh
   • V = (16)(3)(3)
   • V = 144


3. You will add the volumes together to find the total volume.
   
   • 306 + 144 = 450

The total volume of the shape is 450.

Volume of a Cylinder

Let's find the volume of the cylinder below. You will find the area of the base and then multiply it by the height.

You will use the following formula: V = πr²h

1. Fill in all of the information you know into the formula.
   V = πr²h
   
   V = π(4²)(14)



2. Simplify the problem. It is acceptable to leave your answer in terms of pi unless you are told to do something else.
   V = π(4²)(14)
   
   V = π(16)(14)
   
   V = 224π

The volume of this cylinder is 224π.

Volume of a Sphere

Let's find the volume of the sphere below.

You will use the following formula to find the volume: V = 4/3πr³

1. Fill in all of the information you know into the formula.
   V = 4/3πr³
   
   V = 4/3π(8³)



2. Simplify the problem. It is acceptable to leave your answer in terms of pi unless you are told to do something else.
   V = 4/3π(8³)
   
   V = 4/3π(512)
   
   V = 682 2/3 π

The volume of this sphere is 682 2/3 π.

Volume of a Cone

Let's find the volume of the cone below.

You will use the following formula to solve for the volume: V = 1/3 πr²h

1. Fill in all of the information you know into the formula.
   V = 1/3 πr²h
   
   V = 1/3 π(8²)(12)



2. Simplify the problem. It is acceptable to leave your answer in terms of pi unless you are told to do something else.
   V = 1/3 π(8²)(12)
   
   V = 1/3 π(64)(12)
   
   V = 256π

The volume of this cone is 256π.