7.07 Applying Measures of Central Tendency

Learn

Central Tendencies and Grades

In the previous lesson, we found out how to find the measures of central tendency. In this lesson, we are going to look at some real-world applications of these skills.

You are most familiar with mean. As a student, you will receive grade reports from your school with your current averages on them. You most likely have several activities and assignments that have earned grades, and your teacher or the school's software will find the average of these activities and assign you a grade for a course.

Some people think that the mean and the median will be the same thing. This is normally not the case. The median identifies the middle value in the data set. The mean could be skewed, for instance, if you are a student that is lazy for the beginning of a grading period and then works hard toward the end to get a few high grades and pull your average up. If this is the case, your median may likely be a much lower number than your mean. If this is the case, median gives a better representation of central tendency than average.

The mode is the most common number in a data set. This is important to look at when thinking about your grades, as well, because it shows your normal performance. You may have a few grades that are lower or higher but the mode indicates the grade range where you normally, or most often, perform or meet.

Example #1

A math teacher gives her students a survey where they can rate how well they are doing in the class, with 1 being the lowest score (the student feels he/she is failing) and 5 being the highest score (the student feels he/she is acing the course). After all her students completed the survey, the teacher put the data into the chart below. Now, she's going to use measures of central tendency to analyze the data and see how the students in her class feel about their math class performance.

Performance Rating	Number of Students
1	8
2	3
3	3
4	4
5	3

The first thing we want to do is to list the numbers in order from least to greatest: 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5.

Now, let's determine measures of central tendency of this data set.

• The mean is:
  


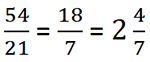
• The median is 2.


• The mode is 1.

This teacher may look at this data and say, "The mean, or average response, is !" Therefore, my students think that they are average. However, if she looks at the mode (which is 1), she can see that a large portion of the class does not think they are doing a good job; in fact, the majority of students in the class rating themselves as failing!

It's important to take all measures of central tendency into account when looking at data sets as the findings of each can be interpreted differently!

Example #2

Understanding how these numbers are computed is important. For example, as a member of your school's basketball team, you need to maintain at least a 70 average to play. Your grades so far are: 68, 72, 60, 78, and 67. What is the least that you can make on the next test to keep a 70 average?

We will let the next test score be x. We use 6 as the denominator because there will be a total of 6 tests.

345 + x = 420

345 − 345 + x = 420 − 345

x = 75

You will need to make at least a 75 on your next test to continue playing!