Learn
Exponential Decay
The function y = abx can also be used to model exponential decay as well as exponential growth where
- a is the starting amount when x=0,
- b is the base which is between 0 and 1 and is the decay factor.
- The C takes the place of the a term and (1 - r) takes the place of the b term.
Examples:
- y = 5(0.93)x and y = 5(0.95)x are equations showing exponential decay
- The function can be modeled by:
- y = C(1 - r)t where C is the original amount, r is the rate of decay and t is the time or number of years.
- y = 5(1 - .03)t and y = 3(1 - .05)t are equations showing exponential decay
Exponential Growth and Decay
The graph below shows the graphs of both exponential growth and decay. The equation y = 3(1 + .07)x is exponential growth (blue line) and the equation y = 3(1 - .07)x is exponential decay (red line).
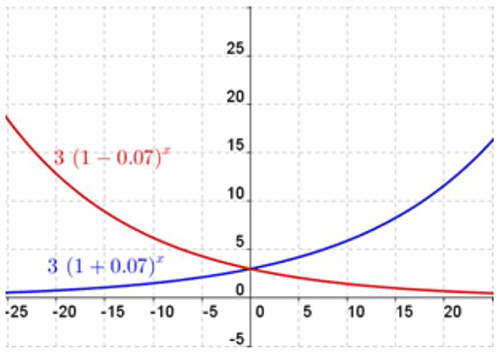
Notice for exponential growth that as x increases, y increases exponentially. For exponential decay as x increases, y decreases exponentially.
Example #1
Open Use Exponential Decay to Model and Solve Real-World Situations in a new tab
Example #2
Open Use Exponential Decay to Model and Solve Real-World Situations in a new tab
Example #3
Open Use Exponential Decay to Model and Solve Real-World Situations in a new tab
Use of Exponential Growth and Decay
You can see from the examples that population growth and decay can be used to predict the future population of an area. This would be useful in urban and regional planning and development of areas.
You also can use exponential growth and decay to determine how much money you need to invest to reach a savings goal over time or how much a decaying investment such as a car will be worth over time.