Learn
Scatter Plot Trends
In this lesson, we are going to look at how to draw a trend line. This can also be referred to as line of best fit.
Remember, we are looking for a relationship between the two things graphed in our scatter plot. We have already talked about positive correlations, negative correlations, and no correlations.
Trend Line
The points in this plot fall in a line. We say that a strong positive association exists between the variables plotted here. This is not normally the case for scatter plots.
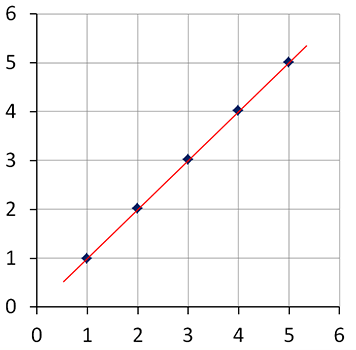
See larger version of graph here.
When drawing the trend line, we should try to place it through the center of the points that have been plotted. Sometimes, we have outliers; an outlier is a point that lies outside the main body that it is a part of the plotted points. If this is the case, you should not consider the outlier when placing your trend line. The outlier in this scatter plot is circled in red.
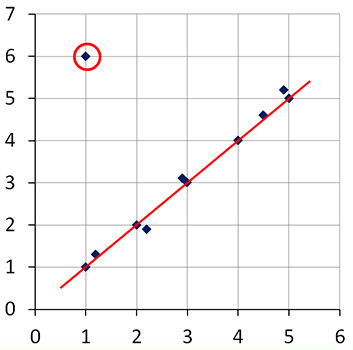
See larger version of graph here.
When deciding where to place your trend line, keep in mind that you should try to have it as close as possible to all points with as many points above it as are below it. Of course, you will not take the outliers into consideration when doing this.
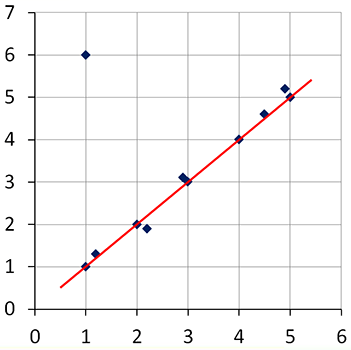
See larger version of graph here.
Equation of a Line
Once you have placed the line, you will want to write an equation of the line.
1. You will first identify two points on the line.
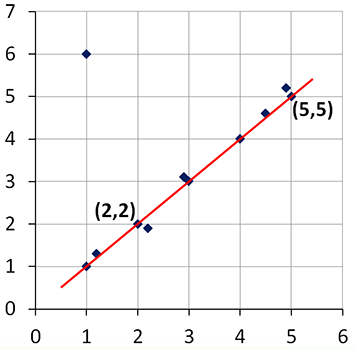
See larger version of graph here.
Slope Formula Equation
2. You will then find the slope using the slope formula:
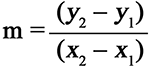
Use (2,2) to fill in (x1,y1) and (5,5) to fill in (x2,y2) in the slope formula.
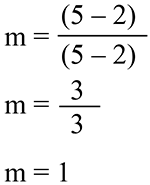
Slope Intercept Equation
If you know the slope and a point on a line, you can use the slope intercept equation to find the y-intercept and then write the equation of the line.
m = 1 passing through (5,5)
y = mx + b
5 = (1)(5) + b
5 = 5 + b
0 = b
y = x

See larger version of graph here.
Slope Intercept Equation Prediction
Even though all of the points do not fall directly on this line, you can use the equation to predict where other points might fall. For instance, if x = 210 then a close prediction could be that y = 210 also (if y = x).

See larger version of graph here.