2.03 Determining Maximum and Minimum Values

Graph Constraints to Determine Max/Min Values

In the previous lesson, we learned to determine maximum or minimum values for an objective function if we were given the graph of the constraints and the feasible region.

In this lesson, the objective function and the system of constraints will be given, and the graph will have to be constructed. Then, as before, the vertices of the feasible region will be used to determine the maximum or minimum value of the objective function.

Example #5

Find the minimum value for the objective function C(x, y) = 100x - 18y given the following constraints:

First, graph the constraints to determine the feasible region.

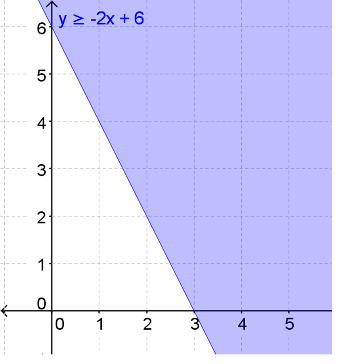
Answer:

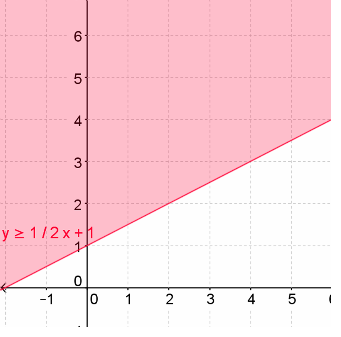
Answer:

Answer:

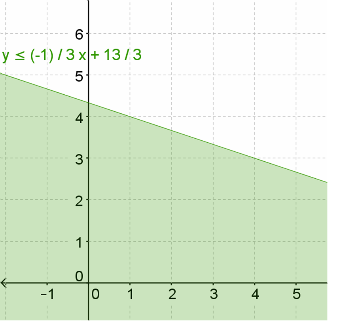
You do not have to use the y-intercept to graph - You can plug in any x, for example x = 1, and solve for Y to get a point, then use the slope from that point to graph the line.

Feasible Region:

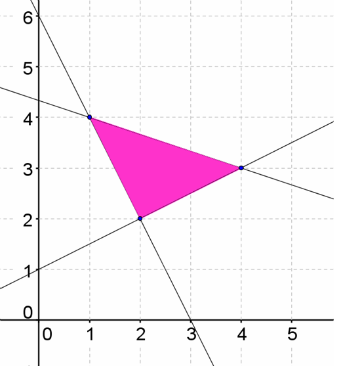
Use the graph to find the vertices of the feasible region.

The feasible region has 3 vertices. The vertices are:

(1,_)

(_,2)

(4,_)

Answer: (1,4), (2,2), (4,3)

Use the graph to find the vertices of the feasible region.
The feasible region has 3 vertices. The vertices are: (1,4), (2,2), (4,3)
Plug these values into the objective function C(x, y) = 100x - 18y to determine the minimum value.

C (1,4) = _

C (2,3) = _

C (4,3) = _

Answer:

C (1,4) = 28

C (2,3) = 164

C (4,3) = 346

Use the graph to find the vertices of the feasible region.
The feasible region has 3 vertices. The vertices are: (1,4), (2,2), (4,3)
Plug these values into the objective function
to determine the minimum value.

C(1,4) = 28
C(2,2) = 164
C(4,3) = 346

The maximum amount is 28 and occurs when x = 1 and y = 4.

Example #6

Find the maximum value for the objective function P(x, y) = 35x - 6y given the following constraints:

x ≥ 0

y ≥ 0

x + y ≤ 30

x + 2y ≤ 40

Graph the constraints.

x ≥ 0

y ≥ 0

x + y ≤ 30

x + 2y ≤ 40

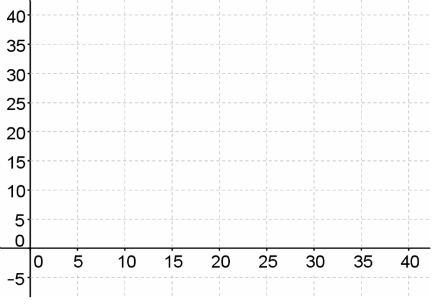
x ≥ 0

Answer:

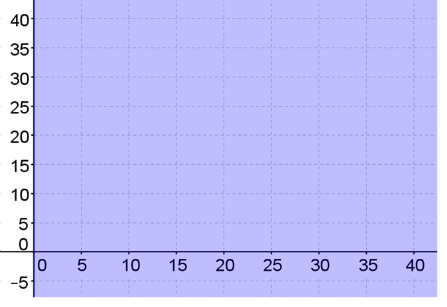
y ≥ 0

Answer:

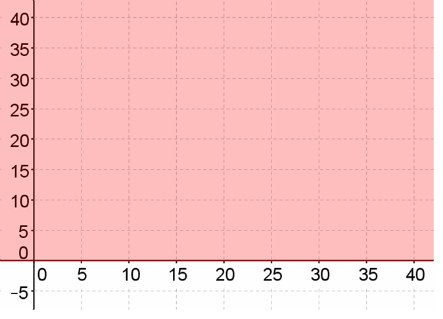
x + y ≤ 30

Answer:

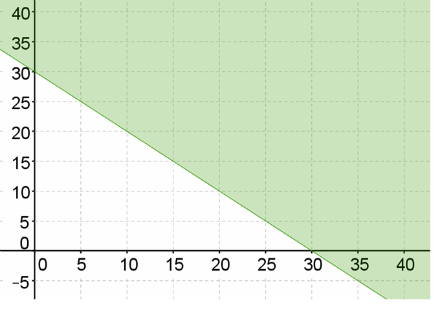
x + 2y ≤ 40

Answer:

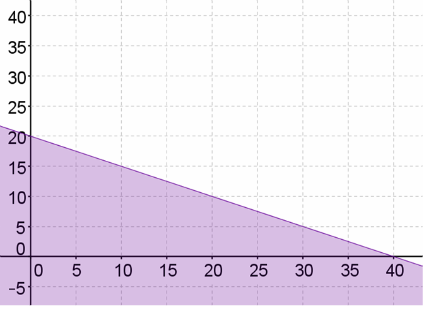Find the feasable region.

Answer:

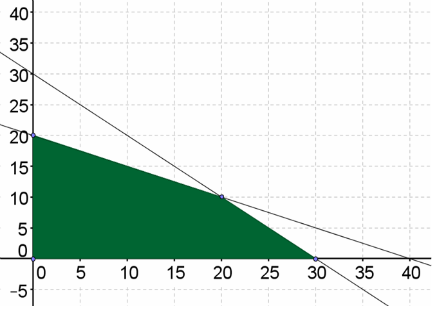
Determine the vertices of the feasible region you graphed.
The region has 4 vertices. The vertices are:
(_ ,_)

(_ ,_)

(_ ,_)

(_ ,_)

Answer:

(0 ,0)

(0,20)

(20,10)

(30 ,0)

Determine the vertices of the feasible region you graphed.
The region has 4 vertices. The vertices are:
(0,0), (0,20), (20,10), and (30,0)

Determine the maximum by substituting these into the objective function P (x,y) = 35x - 6y

P(0 ,0) = _

P(0,20) = _

P(20,10) = _

P(30 ,0) = _

Answer:

P(0 ,0) = 0

P(0,20) = 120

P(20,10) = 640

P(30 ,0) = 1050

The maximum value is 1050 and occurs when x = 30 and y = 0.