"And" Inequalities Examples

There are two methods to solving AND compound inequalities. Most of the time, you will be able to choose which method you would like to use; however, there will be times when you will not be able to choose your method.

The first method is solving the inequality as it is and solving both sides simultaneously. This will only work if your inequality is written as a string of two inequalities.

The second method involves splitting the inequality into two separate inequalities to solve. This method always works.

Example #8

Solve and graph the inequality -10 < a - 7 ≤ -2


Recall the objective for solving any equation or inequality: to isolate the variable. The first method for solving this type of compound inequality is to isolate the variable in place without separating the inequality. In the inequality above, what number should be moved to isolate the variable?


To isolate a, apply the addition property. Since this inequality has three parts, the properties you apply to the expression in the middle will also need to be applied to the outside.

-10 is less than a-7 is less than or equal to -2. Apply addition property to take 7 out of the middle


The second method involves separating the compound inequality into two inequalities:

- 10 < a - 7 and a - 7 ≤ - 2

Solve each inequality using the same property as in the last method. Use the addition property to isolate the variable on both sides.

-10 is less than a - 7. Apply addition property to isolate the variable.

a - 7 is less than or equal to -2. Apply addition property to isolate the variable.

To graph the compound inequality, find the intersection and graph a > -3 and a ≤ 5

Graph of a > -3

Number line: -5,-4,-3,-2,-1,0,1,2,3,4,5,6,7,8 Circles: Open circle on -3 Shading: to the right of -3

Graph of a ≤ 5

Number line: -5,-4,-3,-2,-1,0,1,2,3,4,5,6,7,8 Circle: closed circle on 5 Shading: to the left of 5

Graph the compound inequality.

-10 < a - 7 ≤ -2

Answer:

Number line: -5,-4,-3,-2,-1,0,1,2,3,4,5,6,7,8 Circles: open circle on -3, closed circle on 5. Shading: to the right of -3 and left of 5.

Your left endpoint is an open point at -3 and your right endpoint is a closed point at 5.

Example #9

Solve and graph the inequality 2k + 4 > -14 and -6k + 6 > 30.

In this example, you will have no choice but to use the second method. Recall that the second method is to solve each inequality separately. Begin solving the first inequality by subtracting 4 on both sides.

In this example, you will have no choice but to use the second method. Recall that the second method is to solve each inequality separately. Begin solving the first inequality by subtracting 4 on both sides.

 

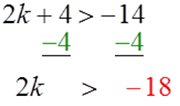
2k + 4 is less than -14. Subtract 4 from both sides, which creates 2k is greater than -18


Use the division property to isolate the variable.

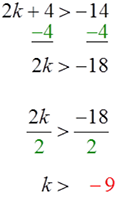
2k is less than -18. Use division property to isolate the variable. k is greater than -9

Solve the second inequality next. Apply the subtraction property to isolate the variable term.

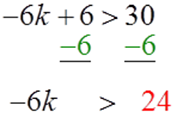
-6k + 6 is less than 30. Subtract 6 from both sides, which creates -6k is greater than 24


Divide both sides by -6 to isolate the variable.
What to remember? - Remember that when you divide or multiply by a negative value, you must flip your inequality sign.

-6k is less than 24. Divide both sides by -6 which equals k is less than -4

After you have solved both inequalities, you will need to graph.

Graph the inequality k > -9

number line with an open circle at -9 and has shading that carries on forever to the right

Graph the inequality k < -4

number line with an open circle at -4 and has shading that carries on forever to the left

Which is the correct graph of the compound inequality?

Answer:

number line with an open circle at -9 and closed circle at -4 with shading in between.

Example #10

Solve the inequality -23 < 5x + 2 ≤ 17

Begin by applying the subtraction property to isolate the variable term. Remember that what you do to the middle must also be done to the outside of the inequality.

- 23 is less than 5x + 2 is less than or equal to 17. Subtract 2 from all sides.

You have to isolate the variable now. Apply the division property to isolate x in the inequality.

-25 divided by 5 is less than 5x divided by 5 is less than or equal to 15 divided by 5

Choose the correct graph of the compound inequality. -5 < x ≤ 3

Answer:

number line with an open circle at -5 and closed circle at 3 with shading in between.

Back Button