"And" Inequalities

You have learned about “or” compound inequalities. In this lesson, you will learn about “and” compound inequalities.

AND compound inequalities are inequalities which have two parts and the solutions will occur between two given values. They can be written with the word and or as one string of two inequalities.

AND inequalities could appear as:

2x - 5 > -15 and 3x < 12 or -24 < 3x + 3 ≤ 15

 

Graphing Compound Inequalities

The graph of an AND inequality will be the intersection between two graphs; meaning, you will graph the overlapping part of the graph.


If you were given the graphs below:

top graph has an open circle at -4 and shading that carries on forever to the right. Bottom graph has a closed circle at 2 and shading that carries on forever to the left. They intersect at -4 and +2.

Their intersection would have a left endpoint at -4 and right endpoind at 2. Your final graph would be the intersection of these two graphs.

Line graph that has an open circle at -4 and closed circle at +2.

Note: -4 would be an open point because it is not shaded in both graphs. The top graph has an open point at -4 and the bottom graph is shaded over -4. The value 2 would be a closed point because it is included in both graphs.

 

Example #6

Graph the inequality -5 ≤ m ≤ 1

This inequality can be split into two separate inequalities: -5 ≤ m and m ≤ 1

The symmetric property can be applied to the first inequality to obtain m ≥ -5

And if you were to graph this inequality, you would have:

numberline: ...-6,-5,-4,-3,-2,-1,-,0,1,2,3,4,5,6... circles: closed cirlce on -5 shading: to the right of -5

 

Graph the inequality -5 ≤ m ≤ 1


If you were to graph the second inequality, m ≤ 1 your graph would look like:

numberline: ...-6,-5,-4,-3,-2,-1,-,0,1,2,3,4,5,6... Circle: closed circle on 1.

 

Graph the inequality: -5 ≤ m ≤ 1


To graph the compound inequality, you would graph the intersection of these two graphs.

Number line: ...-6,-5,-4,-3,-2,-1,-,0,1,2,3,4,5,6... Circles: closed circle at -5 Shading: to the right of -5 Number line: ...-6,-5,-4,-3,-2,-1,-,0,1,2,3,4,5,6... Circles: closed circle on 1 Shading: to the left of 1

What is the left endpoint of your graph?

What is the right endpoint for your graph?


To graph the compound inequality, you would graph the intersection of these two graphs.

two number lines. First one has a closed circle at -5 and shading that continues to the right. The second one has a closed circle at +1 and shading that continues to the left. They intersect at -5 and +1.

The blue lines show the intersection of the two graphs so the graph of the compound inequality is:

Number line: ...-6,-5,-4,-3,-2,-1,-,0,1,2,3,4,5,6... Circles: Closed circles at -5 & 1 Shading: in between -5 and 1

 

Example #7

3 < m ≤ 9

To graph the first inequality, apply the symmetric property to rewrite the inequality as m > 3 and graph this inequality.

Number line: 0,1,2,3,4,5,6,7,8,9,10

 

Then, graph the second inequality, m ≤ 9

 

Number line: 0,1,2,3,4,5,6,7,8,9,10 Circles: closed circle on 9 Shading: to the left of 9

 

What is the correct way to graph this compound inequality?

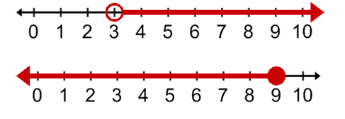
Number line 1: ...0,1,2,3,4,5,6,7,8,9,10... Circle 1: open circle on 3 Shading 1: to the right of 3 Number line 2: ...0,1,2,3,4,5,6,7,8,9,10... Circle 2: closed circle on 9 Shading 2: to the left of 9

Answer:

Number line:...0,1,2,3,4,5,6,7,8,9,10... Circles: open circle on 3, closed circle on 9 Shading: in between 3 and 9

 

Back Button