"Or" Inequalities Examples

Solving compound inequalities is very similar to solving single inequalities. The only difference with compound inequalities is that you will have two separate parts to solve.

With “or” compound inequalities, keep in mind the solution to the inequality is a value that makes either of the individual inequalities true.

Example #3

Solve the inequality 6m – 8 > 4 or 6m + 2 < -4.

You will solve each of these separately.
Begin with the first inequality, 6m – 8 > 4.

Add 8 to both sides to begin to isolate the variable term.

6m - 8 is less than 4. Add 8 to both sides to isolate the variable term.

Divide both sides by 6 to isolate the variable.

6m divided by 6 is greater than 12 divided by 6

Next, solve the second inequality.

Subtract 2 from both sides to isolate the variable term.

6m +2 < -4

+2 -2

Use the division property to isolate the variable.

6m divided by 6 is less than -6 divided by 6.

Now, you have the solution to both inequalities: 6m < -6 and m < -1

Graph the solution to the compound inequality
6m – 8 > 4 or 6m + 2 < -4.

Graph the solution to the inequality for m > 2 or m < -1:

Answer:

number line: -5,-4,-3,-2,-1,0,1,2,3,4,5 Circle: Open circle at -1, open cirlce at 2. Shading: away from the middle

 

Example #4

Solve the inequality 2x < -10 or (x/3) is greater than or equal to..-1

Remember to work with each inequality separately.

Solve the first inequality for x. 2x < -10

Divide by 2 on both sides.

2x divided by 2 is less than -10 divided by 2

Next, solve the second inequality. Multiply on both sides by 3 to isolate the variable.

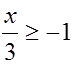
(x/3) is greater than or equal to -1

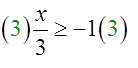
(3)(x/3) is greater than or equal to -1(3)


Your solutions are x < -5 and x ≥ -3. Graph the solution.

Answer:

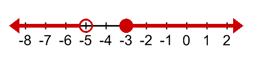
Number line: -8,-7,-6,-5,-4,-3,-2,-1,0,1,2

Explained: You have an open point at -5 with shading to the left. You have a closed point at 3, with shading to the right.

Example #5

Solve the inequality -6a + 6 ≤ -18 or a - 6 ≤ -8

Remember to work with each inequality separately.
Start by solving -6a + 6 ≤ -18.

Apply the subtraction property to isolate the variable term.

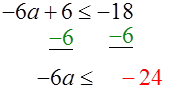
-6a + 6 is less than or equal to -18 substract 6 from both sides. this gets rid of the 6 on the left side of the equation and changes -18 to -24 on the right side of the equation. After the operation is complete the equation is left at -6a is less than or equal to -24.

Next, isolate the variable, a, by applying the division property.

-6a divided by -6 is less than or equal to -24 divided by -6

Now, solve the other side: a - 6 ≤ -8 . The variable does not have a coefficient, so we only need to add 6 to both sides of the inequality.

a - 6 is less than or equal to -8. Add 6 to both sides to isolate the variable.

You now have the answer to both inequalities.

a ≥ 4 and a ≤ -2

Your solutions are greater than or equal to 4 and less than or equal to -2. Graph the solution.

Answer:

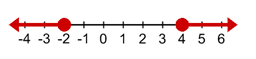
number line: -4,-3,-2,-1,0,1,2,3,4,5,6

Explained: You have a closed point at 4 with shading to the right. You will also have a closed point at -2, with shading to the left.

Back Button