Compound Inequalities
A compound inequality is an inequality which joins two or more inequalities using the words “and” or “or”. You will learn more about “and” inequalities in the next lesson.
An OR inequality represents the union of two inequalities. Its graph will appear as:
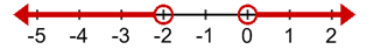
"OR" Inequalities
Compound inequalities that contain the word or are true if one or more of the inequalities is true. Think about the example
n < -4 or n > 2. If you have an or inequality, it will always contain the word or in the inequality.
The graph of n < -4 or n > 2 will produce two shaded regions on the graph. There will be an open circle at -4 and 2. The graph will be shaded to the left of -4 as well as to the right of 2.
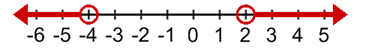
The graph of n < -4 or n > 2 shows that the true solutions are less than -4 and greater than 2.
We cannot have a solution of -4 or 2 because inequalities do not contain an equal sign. Therefore, they are not included in the solutions.
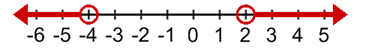
Example #1
Graph the inequality x > 5 or x ≤ -1
At 5, you will have an open point with shading to the right.
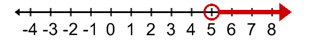
At -1, you will have a closed point with shading to the left.
The complete graph will include both solutions:

Example #2
Graph the inequality x ![]() 4 or x > 6
4 or x > 6
At 4, you will have a closed point with shading to the left.

At 6, you will have an open point with shading to the right.
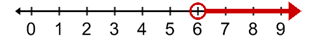
The complete graph will include both solutions: