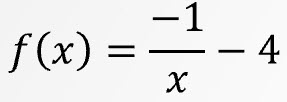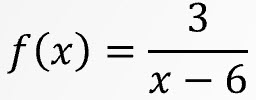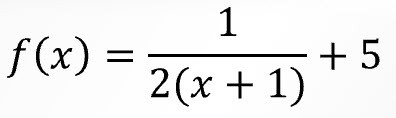Learn

Reciprocal Functions

All reciprocal functions can be graphed using the parent function \left(x\right)=\frac{1}{x\ } and paying attention to the key features, which are: domain, range, x asymptote, y asymptote, center of the function.

Transforming Reciprocal Functions

Translate 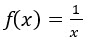\left(x\right)=\frac{1}{x\ }Up 2 Units

Graphically: Move the hyperbola up 2 units.

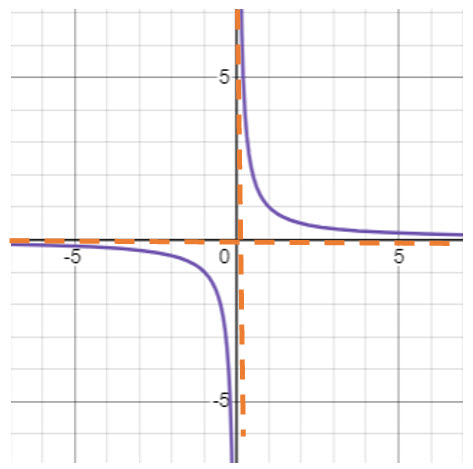
Original: \left(x\right)=\frac{1}{x\ }

Algebraically: Add 2 to: \left(x\right)=\frac{1}{x\ }+ 2

Note: Vertical shifts require you to add or subtract from f(x). f(x) – c Down and f(x) + c Up.

Vertical Shift Key Features

Vertical Shift Key Features
Original Tranformation
Center: (0, 0) Center: (0, 2)
y asymptote: x = 0 y asymptote: x = 0
x asymptote: y = 0 x asymptote: y = 2
Domain: (–∞, 0) U (0, ∞) Domain: (–∞, 0) U (0, ∞)
Range: (–∞, 0) U (0, ∞) Range: (–∞, 2) U (2, ∞)
Odd: Yes Odd: No

Notice that a vertical shift caused the center, horizontal asymptote, and the lines of symmetry to move up 2 units.

 

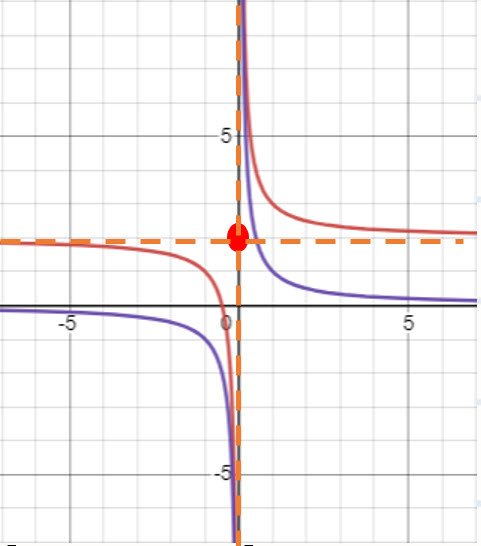
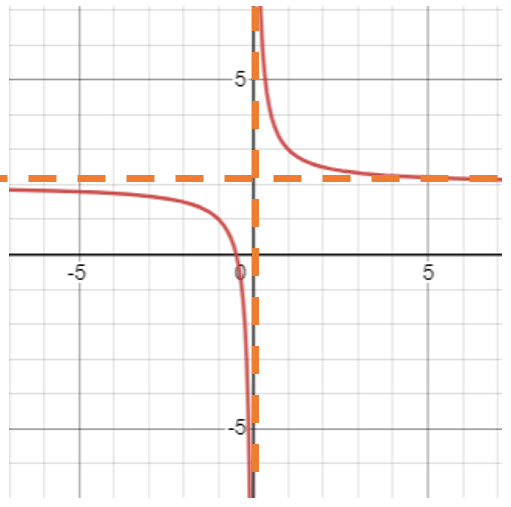
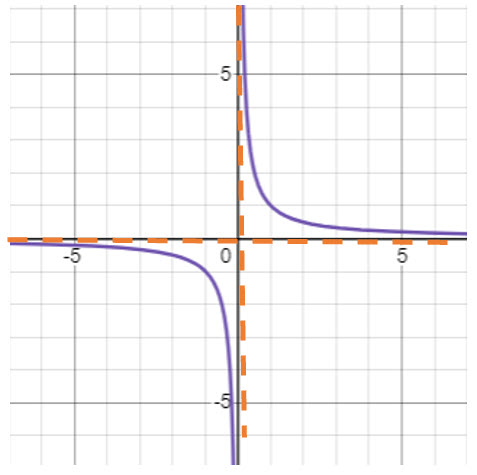
Translate 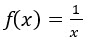\left(x\right)=\frac{1}{x\ }Right 2 Units

Graphically: Move the hyperbola right 2 units.

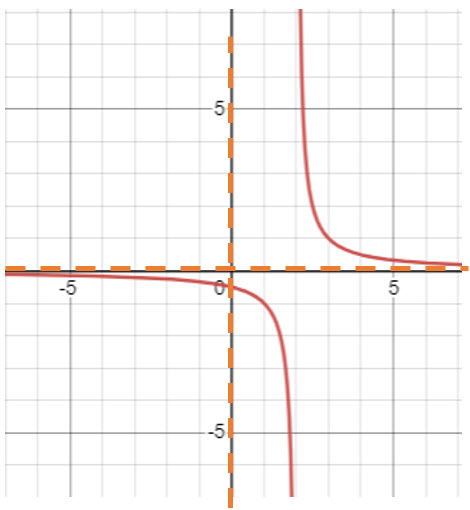
Original: \left(x\right)=\frac{1}{x\ }

Algebraically: Subtract 2 from x:\left(x-2\right)=\frac{1}{x-2\ }+ 2

Note: Horizontal shifts require you to add or subtract from x. f(x – c) Right and f(x + c) Left.

Horizontal Shift Key Features

Horizontal Shift Key Features
Original Tranformation
Center: (0, 0) Center: (2, 0)
y asymptote: x = 0 y asymptote: x = 2
x asymptote: y = 0 x asymptote: y = 0
Domain: (–∞, 0) U (0, ∞) Domain: (–∞, 2) U (2, ∞)
Range: (–∞, 0) U (0, ∞) Range: (–∞, 0) U (0, ∞)
Odd: Yes Odd: No

Notice that a horizontal shift caused the center, horizontal asymptote, and the domain to move right 2 units.

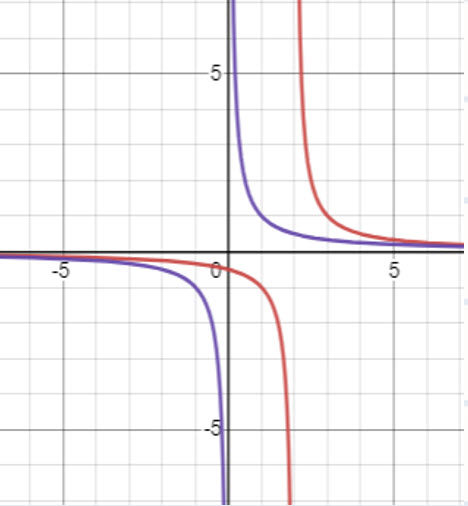
Stretch 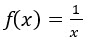\left(x\right)=\frac{1}{x\ }by a Factor of 2

Graphically: Stretch the graph vertically by 2 units.

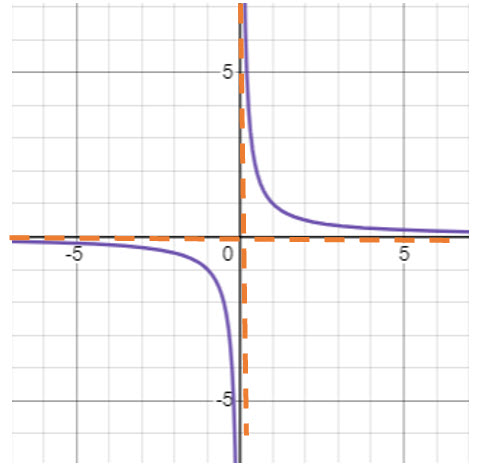
Original: \left(x\right)=\frac{1}{x\ }

Algebraically: Multiply by 2

Transformation: \left(x\right)=\frac{2}{x\ }

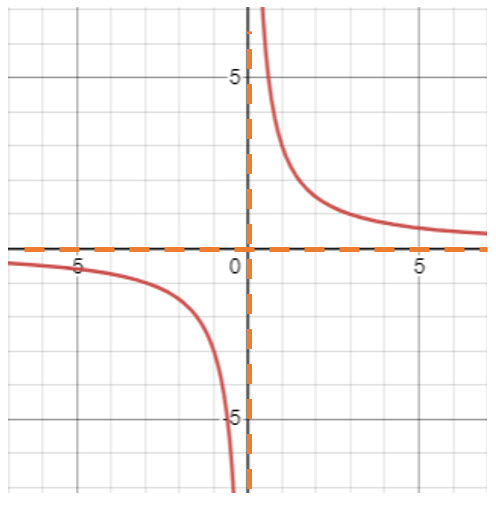
Note: Horizontal shifts require you to add or subtract from x. f(x – c) Right and f(x + c) Left.

Stretch and Shrink Key Features

Stretch and Shrink Key Features
Original Tranformation
Center: (0, 0) Center: (0, 0)
y asymptote: x = 0 y asymptote: x = 0
x asymptote: y = 0 x asymptote: y = 0
Domain: (–∞, 0) U (0, ∞) Domain: (–∞, 0) U (0, ∞)
Range: (–∞, 0) U (0, ∞) Range: (–∞, 0) U (0, ∞)
Odd: Yes Odd: Yes

Notice that during a stretch or shrink the key features remain the same.

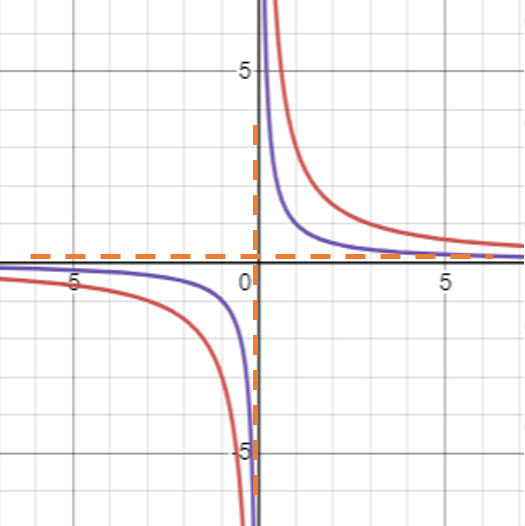
Standard Reciprocal Equation

f(x)=\frac{a}{x-h}\ +k

  • a > 1 vertical stretch
  • –a reflection over the x-axis
  • k > 0 translates functin up by k units
  • h > 0 translates functin right by h units
  • 0 < a < 1 shrink (horizontal stretch)
  • –x reflection over the y-axis
  • k < 0 translates function down by k units
  • h < 0 translates function left by k units

Examples

Write a reciprocal function for the transformation below.

  1. Translates the function down 4 and reflected over the x-axis.
    • f of x equals negative 1 over x minus 4
  2. Translates the function right 6 and stretched by a factor of 3.
    • f of x equals the fraction with numerator 3 and denominator x minus 6
  3. Translates the function left 1, up 5 and shrinks it by a factor of ½.
    • f of x equals 1 over 2 times open paren x plus 1 close paren plus 5