Learn

Trigonometric Ratios

Recall: The sum of all three angles in a triangle equals 180° The Pythagorean Theorem is used for the sides of a right triangle a2 + b2 = c2

Now for our study of Trigonometry (also known as Trig ), which begins by relating the sides and angles of a right triangle. Definitions are extremely important in this section!

Vocabulary

  • sine
  • cosine
  • tangent
  • cosecant
  • cotangent
  • opposite side
  • hypotenuse
  • SOH-CAH-TOA

Sum of Interior Angles

The sum of ALL three angles in a triangle is 180°.

a right triangle A B C angle C is the right angle
m∠A + m∠B + m∠C = 180°

Pythagorean Theorem

The relationship between the sides of a right triangle is a² + b² = c² where a and b are the legs of the right triangle and c is the hypotenuse.

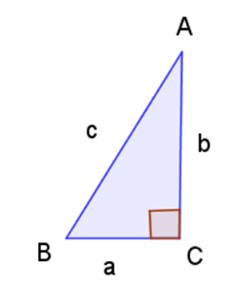
right triangle A C B segment A B is labeled c, segment A C is labeled b, segment C B is labeled a, angle C measures 90 degrees

The angles opposite each side are labeled with the same letter. So, angle A is opposite side a, angle B is opposite side b, and angle C is opposite the hypotenuse. Notice how the sides are labeled with lower case letters and the angles with upper case letters.

Trigonometric Ratios

Now that we know how to name all of the sides, let’s talk about how we will refer to them in trig ratios. First we identify the acute angle we are going use to relate to the sides of the triangle.

So let’s use ∠A . The easiest side to identify is the hypotenuse because it is always across from the right angle. So the hypotenuse is c, leg opposite to ∠A is a, leg adjacent to ∠A is b.

Notice how the legs are identified if we choose to use the acute angle ∠B.

So the hypotenuse is still c, but leg opposite to ∠B is b, leg adjacent to ∠B is a.

Trig Functions

There are six trig functions we will learn. They will be abbreviated as:

  • Sine = sin
  • Cosine = cos
  • Tangent = tan
  • Cosecant = csc
  • Secant = sec
  • Cotangent = cot

Trig Functions Definitions

The trig functions relate sides of a function to the angles of a triangle. In this course, we will only look at trig functions in right triangles. Take a look at the definitions below.

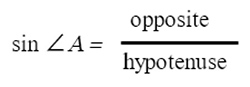
sin angle A = opposite/hypotenuse
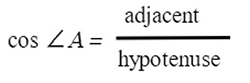
cos angle A = adjacent/hypotenuse
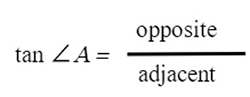
tan angle A = opposite/adjacent

Let’s look at the next three trig functions. Notice they are the inverse of the first three.

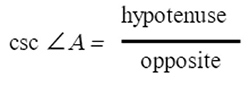
csc angle A = hypotenuse/opposite
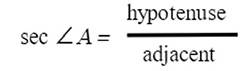
sec angle A = hypotenuse/adjacent
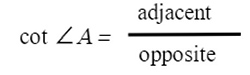
cot angle A = adjacent/opposite

How to Remember?

You may want to use the mnemonic device to help you remember these three trigonometric functions and their ratios.
SOH – CAH – TOA (SŌH – CĂH – TŌA)
This means: Sine is opposite over hypotenuse Cosine is adjacent over hypotenuse Tangent is opposite over adjacent
If this is too hard try this sentence:
Some Old Hippie Caught Another Hippie Teaching Old Algebra

Reciprocals

Notice how these pairs of trig functions are reciprocals.

two arrows making an x between sin angle A = opposite/hypotenuse and csc angle A = hypotenuse/opposite
two arrows making an x between cos angle A = adjacent/hypotenuse and sec angle A = hypotenuse/adjacent
two arrows making an x between tan angle A = opposite/adjacent and cot angle A = adjacent/opposite

Example #2

Open Find Trigonometric Ratios of Acute Angles of Right Triangles in a new tab

Example #3

Open Find Trigonometric Ratios of Acute Angles of Right Triangles in a new tab

Example #4

Find Cos ∠B

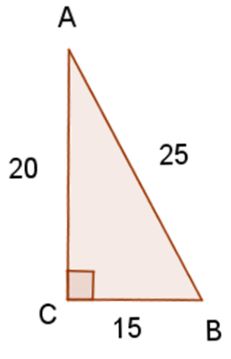
Triangle A C B, A B equals 25. A C equals 20. C B equals 15. Angle C measures 90 degrees.

In some problems, you may be asked to only find one of the six trig functions. Let’s start by identifying the angle.

Now, let’s identify the relationship of the sides in:
adjacent side = BC; opposite side = AC; hypotenuse = AB

Now that we know the relationships of the sides to ∠B, we can substitute the given information into our function.

Remember, cosine is adjacent over hypotenuse. What is the value of BC, the side adjacent to angle B? What is the measure of the hypotenuse, AB?

Be sure to identify the angle first, then the side relationships, finally the trig function definition!

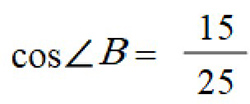
cos angle B = 15/25
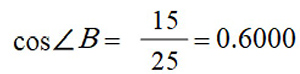
cos angle B = 15/25 = 0.6000

Using a Trig Table

In the introduction activity, notice that when the triangles are similiar the trig ratio did not change even though the slide lengths changed. Therefore we can use a table to find the approximations for each tri ratio if we know the angle.

Trigonometry Tables

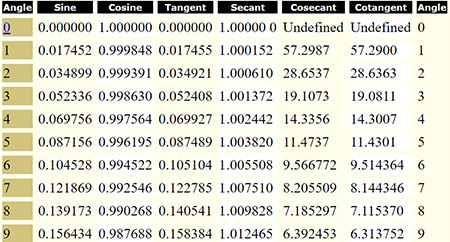
a trigonometry table that lists the trigonometric values for angle measures 0 to 9 degrees.

Using a Trig Table Example

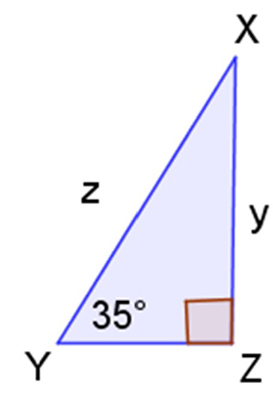
As long as you know the measure of an angle, you can find the trig ratio without knowing the sides. Let’s look at this example. Start by identifying the angle and the sides.

Triangle X Z Y, X Z equals y. Y X equals z. Angle Z measures 90 degrees
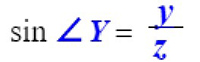
sin angle Y = y / z
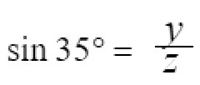
sine 35 degrees = y / z

approximately because the trig function is rounded

Since 35° is the same for all similar right triangles, we will use a chart.

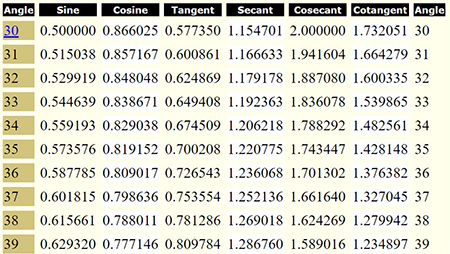
a trigonometry table that lists the trigonometric values for angle measures 30 to 39 degrees.

You start by clicking on the appropriate row for the angle.

Now, identify the column for the appropriate function.

sin 35° = 0.573576

The value of a trig function of a angle is usually given to four decimals places (0.3124) or three places if its absolute value is greater than one (1.312).

Exercise #5

Find the value of Cos 33° using the table below. Be sure to round you answer to the appropriate decimal places.

a trigonometry table that lists the trigonometric values for angle measures 30 to 39 degrees.

Answer: 0.8387

Exercise #6

Find the value of Sec 57° using the table below. Be sure to round you answer to the appropriate decimal places.

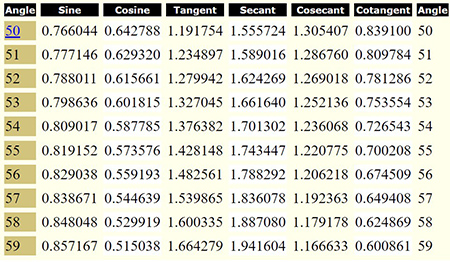
a trigonometry table that lists the trigonometric values for angle measures 50 to 59 degrees.

Answer: 1.836

Example #7

Open Find Trigonometric Values of an Angle Using Desmos Scientific Calculator in a new tab