Introduction
In this lesson, we will look at the graphs of cosecant and secant.
We will relate these graphs to sine and cosine, respectively. Remember that cosecant and secant are the reciprocal functions of sine and cosine. Therefore,
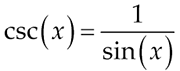
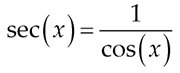
Based on the asymptotes occurring where tangent and cotangent were undefined, what can you conclude about cosecant and secant?
Following successful completion of this lesson, students will be able to...
- Determine the period of cosecant and secant.
- Graph cosecant and secant in the coordinate plane.
Enduring Understandings
- Properties of similar triangles allow us to define the trigonometric ratios.
- Positive and negative angles of all sizes can be represented on the unit circle.
- Proportional relationships express how quantities change in relationship to each other. The trigonometric functions are ratios.
- Students develop skills to solve real world problems modeled by trigonometric functions.
- The graphs of sine and cosine model real-world phenomena.
- The trigonometric functions describe periodic phenomena.
- The x and y coordinates of an answer on the unit circle can be used to find the value of trigonometric functions.
The above objectives correspond with the Alabama Course of Study: Algebra II with Statistics standards: 30c and 40.