6.06 Graphs of Logarithms

Learn

Graphs of Logarithms

After completing the Introduction of this lesson, you should remember the exponential and logarithm graphs are inverses.

An inverse in its simplest form swaps the x and y cordinates. You should also realize that the domain and range of these graphs have swapped.

Let’s look just a little deeper.

Study the graphs below of logarithm graphs with base 2, 10, e.

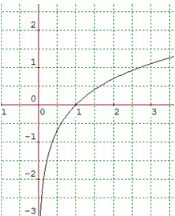
y = ln x

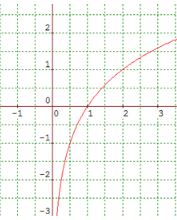
y = log₂x

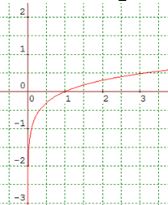
y = logx

Example #1

Use translations to graph f(x) = log(x − 2) + 3

Do you recall that the 2 in the equation moves the graph 2 units to the right and that the 3 moves the graph 3 units up?

Start with the parent graph.

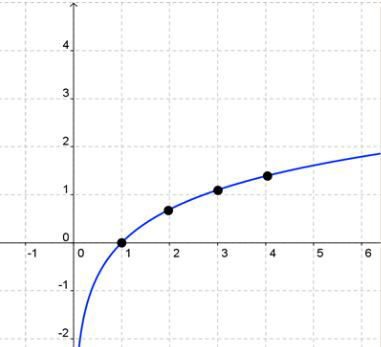
Select points and move them 2 units to the right and 3 units up.

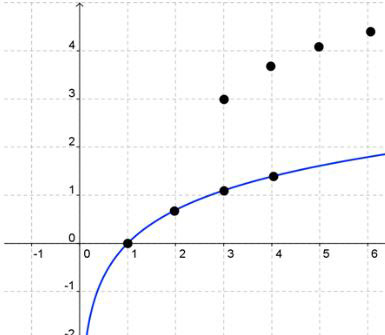
Form the curve of the new graph.

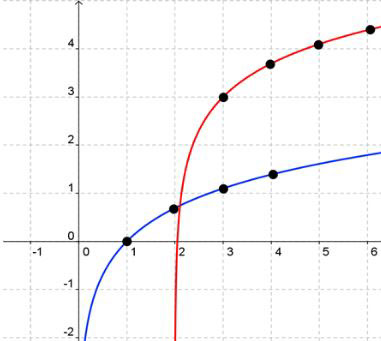
Give the domain, range, and asymptotes of the new graph and describe the end behavior.

• Domain: x > 2
• Range: all real numbers
• Asymptote: x = 2
• x-intercept: 2
• y-intercept: none
• As x appraoches 2 from the left, the graph tends to negative infinity and as x appraoches positive infinity on the right the graph tends to positive infinity.

Example #2

Solve ln 2(x + 4) = 3 by graphing using a graphing utility and verify using a calculator.

Remember how we made a system of equatoins from our problem in previous lessons?

y = 3 and y = ln 2(x = 4) will be our system.

Graph each on the same coordinate plane.

Graph: y = 3 and y = ln 2(x + 4) and locate the intersection.

Use GeoGebra and then sketch your graphs to check.

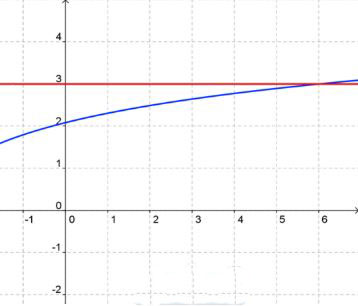
The intersection is (6 , 3). The solution to the problem is x = 6

Now, let’s verify by substituting our solution into the original equation.

ln 2(x +4) = 3

ln 2(6 + 4) = 3

Substitute in the value of x, 6.

Now, let’s verify.
ln 2(x +4) = 3

ln 2(6 + 4) = 3

Simply the argument, then use your calculator. Go to 4 decimal places.

ln 20 = 2.9957

which rounds to 3.00