Try It
Practice Problem #1
Verify that f (x) = 2x + 3 and g(x) = 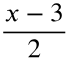 are inverses
are inverses
First, we need to show that f (g(x)) = x.
f(g(x)) = 2 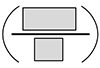 + __
+ __
= (__) + __
= __
Answer:
f(g(x)) = 2 (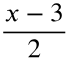 ) + 3
) + 3
= (x - 3) + 3
= x
Next, we need to show that g (f(x)) = x
g(f(x)) = 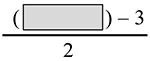
= 
= __
Answer:
g(f(x)) =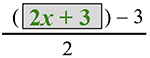 cancel out the 3s - Because both f (g(x)) and g(f(x)) = x, we can conclude that f(x) and g(x) are inverses.
cancel out the 3s - Because both f (g(x)) and g(f(x)) = x, we can conclude that f(x) and g(x) are inverses.
= 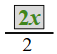 cancel out the 2s
cancel out the 2s
= x
Practice Problems #2
Find the inverse of f(x) = 6 + 5x2. Explain each step and verify that it is an inverse.
f(x) = 6 + 5x - Replace f(x) with y.
y = 6 + 5x2
__ = 6 + 5__2 - Swap x and y - definition of an inverse
Answer: x = 6 + 5y2
__ = 5y2 -Subtract 6 from both sides - subtraction property of equality
Answer: x - 6 = 5y2
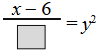
Divide both sides by 5 - division property of equality
Answer:
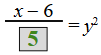
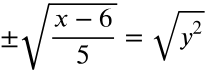 -Take the square root of both sides - inverse operation
-Take the square root of both sides - inverse operation
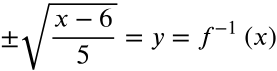
Verify that this is an inverse of f(x) = 6 + 5x2 and f-1(x) = 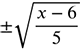 . Find f(f-1(x)).
. Find f(f-1(x)).
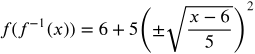 Substitute f -1(x) for x
Substitute f -1(x) for x
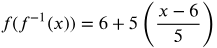 Apply the exponent
Apply the exponent
f(f-1(x)) = 6 + __ - __ = x
Answer:
f(f-1(x)) = 6 + x - 6 = x
f(f-1(x)) = __
Answer:
f(f-1(x)) = x
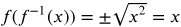
Is this verified?
Answer: Yes
Verify that this is an inverse of f(x) = 6 + 5x2 and f-1(x) = 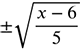 . Find f-1(f(x)).
. Find f-1(f(x)).



f-1(f(x)) = ±x
Is this verified?
Answer: Yes
Practice Problem #3
Find the inversion of 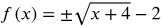 . Explain each astep and verify that it is an inverse.
. Explain each astep and verify that it is an inverse.
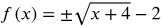
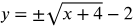 Replace f(x) with y
Replace f(x) with y
 Swap x and y - definition of an inverse
Swap x and y - definition of an inverse
Answer:

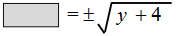 Add 2 to both sides - additive property of equality
Add 2 to both sides - additive property of equality
Answer: 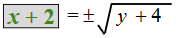
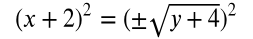 square both sides - inverse operation
square both sides - inverse operation
(x + 2)2 = y + 4
(x + 2)2 __ = __
Answer:
(x + 2)2 - 4 = y
Find the inversion of 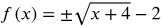 and (x + 2)2 - 4 = f -1(x). Find f(f-1(x)) and and f-1 (f(x))
and (x + 2)2 - 4 = f -1(x). Find f(f-1(x)) and and f-1 (f(x))
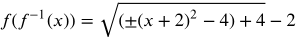 Substitute f -1(x) for x
Substitute f -1(x) for x
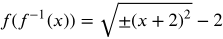 Combine like terms
Combine like terms
f(f-1(x)) = (___) - 2
Answer: x+2
f(f-1(x)) = __
Answer: x
Is this verified? __
Answer: Yes
Find f-1 (f(x))
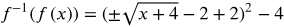 Substitute f -1(x) for x
Substitute f -1(x) for x
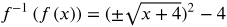 combine like terms
combine like terms
f(f -1(x)) = (__) - 4
Answer: x + 4
f(f -1(x)) = __
Answer: x
Is this verified?___
Answer: yes