Learn
Inverse Functions
Still a Function?
The Introduction should have given you an idea of how functions are related to their inverses. Now let's dig a little deeper.
Is the inverse of a function also a function? Not necessarily. You must test the inverse to determine if it is still a function. In the mapping here, if we swap the domain and range which is what an inverse does, we should have the element 15, paired with a 3 and a 4 and that would make it "not a function".
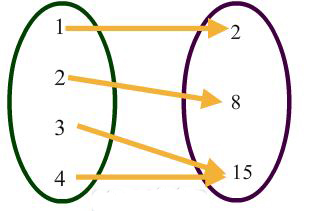
swapped:
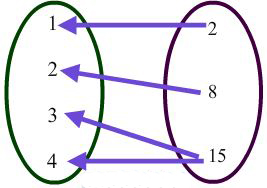
element 15, paired with a 3 and a 4:
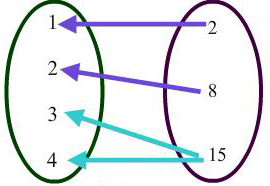
Inverse:
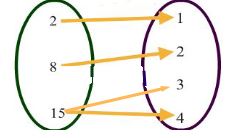
Inverse
If the inverse is a function, then it can be written f -1(x). The -1 seen in the inverse is not an exponent, it just means "inverse." It is read "f inverse" or the "inverse of f."
In all of algebra, the main thing we are trying to accomplish is to find unknowns by solving equations. In other words, solve for x or get x by itself. From the very simplest equation, x + 5 = 9, to the most complex of all, we isolate the x by using inverses. We occasionally say do the opposite but it is actually the opposite operation that we must do and that is really the inverse.
Let's take a look at a few familiar inverses and then we will be looking at more.
In x + 5 = 9, what would you do to get x by itself (some say "Undo" + 5)? ____
Answer: Subtract 5
In 2x = 14, what would you do to get x by itself? ___
Answer: Divide by 2
Subtraction is the inverse of addition and division is the inverse of multiplication.
In x2 = 48, what would you do to get x by itself? ____
Answer: Take the square root
All quadratic equations in one variable are parabolas. What does the inverse, the square root graph look like?
Complete this GeoGebra Quadratic Equation and its Inverse Activity
From the activity, did you discover that the inverse is a flip across the identity line? Click the identify check box and then click the inverse.
Is the inverse a function? (Use the vertical line test) ___
Answer: No
Square Root Function
In x2 = y, we take the square root of both sides and get 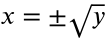 . This is the square root graph, but it is not a function.
. This is the square root graph, but it is not a function.
In order to have a square root function, we define it as the positive part only called the principal square root. Since an inverse "swaps" the x and y, we get 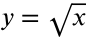 . This is the square root function. The square root function is more feasible when x represents things like length and time since those quantities cannot be negative.
. This is the square root function. The square root function is more feasible when x represents things like length and time since those quantities cannot be negative.
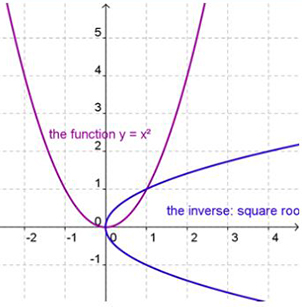
Inverse means swap the domain and the range (the x and the y). In a linear function, the inverse is also a linear function and the domain and range remain the same. What is the domain and range of our square root function, 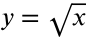 ?
?
This is the graph of the square root function.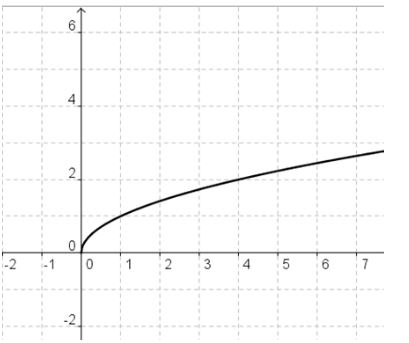
What is the domain and rand of our square root function, 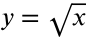 ?
?
Look at the graph. There are no numbers graphed less than 0 on the x axis or the y axis. This tells us the domain is {x ≥ 0}. It also tells us the range is {y ≥ 0}.
How does this relate to the equation?
Answer: For all real values of x, the domain and range for the equation is the same as the domain and range of the graph.
Can x ever be negative?
Answer: No
Can you take the square root of a negative number?
Answer: No. You cannot take the square root of a negative number because by definition square root means a number multiplied by itself to get the answer. Two negatives multiplied together always gives a positive.
Can y ever be negative?
Answer: No. y can be negative when we take a square root, but in order for it to be defined as a FUNCTION, y is greater than or equal to to zero and cannot be negative.
Is there a number that you can the square root of and get a negative?
Answer: No
Process of Finding the Inverse
Finding the inverse is a simple process, but verifying can be rather lengthy.
Steps for finding the inverse of a function:
- Change the f(x) = to y =
- Swap the x and y
- Solve the y and simplify
Example #1
Watch Find the Inverse of a Function.
Open Find the Inverse of a Function in a new tab
Note: The presentation may take a moment to load.
Verifying Inverse Functions
To verify that two functions are inverses of each other, you must show that the composition of each function equals x.
To verify that f (x) and g (x) are inverse functions, you must how that
f (g (x)) = x AND g (f (x)) = x
Example #2
Watch Verify That Two Functions are Inverses of Each Other.
Open Verify That Two Functions are Inverses of Each Other in a new tab
Note: The presentation may take a moment to load.
Example #3
Watch Find the Inverse of a Function; Verify That Two Functions are Inverses of Each Other.
Note: The presentation may take a moment to load.
Example #4
Watch Find the Inverse of a Function.
Open Find the Inverse of a Function in a new tab
Note: The presentation may take a moment to load.