Introduction

Inverse

One thing we did not study in detail with our functions was the inverse.

With an inverse, if you truly understood just the definition, you would understand if from all perspectives - equations, graphs, mappings, ordered pairs.

Let’s take a look. We will start with ordered pairs. Study the functions and inverses below and see if you can find a connection.

Function: {(3,9), (2,8), (4,10), (1,7)}
Inverse: {(8,2), (10,4), (7,1), (9,3)}

Function: {(-1,5), (-2,4), (-4,2), (-5,1)}
Inverse: {(4,-2), (1,-5), (5,-1), (2,-4)}

Mappings

Now, study these functions and inverse and see if you can find a connection.


Function x and Inverse

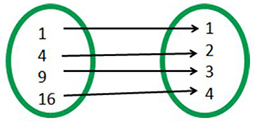
A mapping with 1,4, 9, and 16 in the left circle with arrows going to the mapping on the right with the numbers 1,2,3, and 4. 1 has an arrow going to the 1, 4 has an arrow going to the 2, 9 has an arrow going to the 3 and the 16 has an arrow going to the 4.

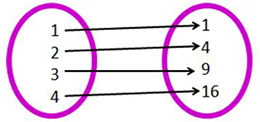
A mapping with 1,2,3, and 4 in the left circle with arrows going to the mapping on the right with the numbers 1,4,9, and 16. 1 has an arrow going to the 1, 2 has an arrow going to the 4, 3 has an arrow going to the 9 and the 4 has an arrow going to the 16.

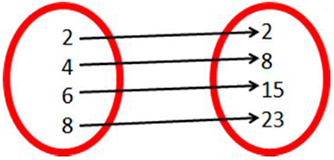
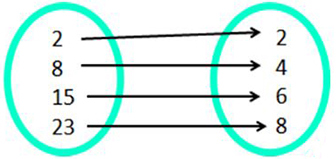
Function f(x) and Inverse

A mapping with 2,4,6, and 8 in the left circle with arrows going to the mapping on the right with the numbers 2,8,15, and 23. 2 has an arrow going to the 2, 4 has an arrow going to the 8, 6 has an arrow going to the 15 and the 8 has an arrow going to the 23.

A mapping with 2,8,15, and 23 in the left circle with arrows going to the mapping on the right with the numbers 2,4, 6, and 8. 2 has an arrow going to the 2, 8 has an arrow going to the 4, 15 has an arrow going to the 6 and the 23 has an arrow going to the 8.

Graphs

The following graphs show a function and an inverse on each coordinate plane. Study them and try to find a connection

Graph 1

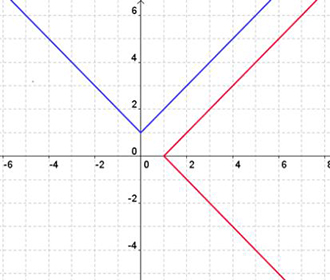
A graph of an absolute value function which looks like a V opening up with a vertex at (0,1). On the same coordinate plane, there is a sideways V graphed opening to the right with a vertex at (1,0). The two graphs are reflected over the line y = x.

Graph 2

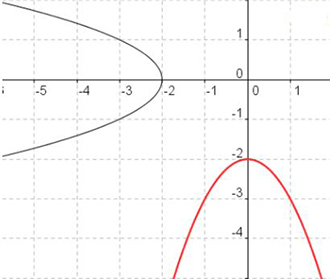
A graph of a parabola y equals negative x squared minus 2 opening down with a vertex at (0,negative 2). On the same coordinate plan is the graph of y = the square root of x plus 2 and y = negative square root of x plus 2. Together, these make a sideways U with a vertex at (negative,0) and opening to the left. These graphs are reflected over the line y=x.

Graph 3

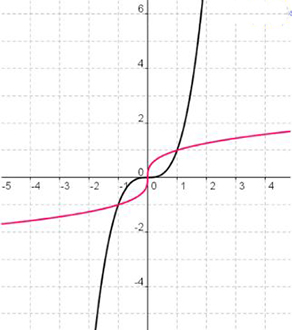
A graph of a parabola y equals x cubed vertex at (0,0). On the same coordinate plan is the graph of y = the cube root of x with a vertex at (0,0). These graphs are reflected over the line y=x.

Inverse Functions

In your observations, I am sure you found connections between the function and the inverse for each one given. What we really need to do is find the same connection between each function and inverse regardless of whether it is a mapping, graph, or set of ordered pairs. Answer the following questions from your observations.

With ordered pairs, what is the connection between the function and its inverse?

Answer: The order pairs were swapped.

With mappings, what is the connection between the function and its inverse?

Answer: The x and f(x) were swapped.

With graphs, what is the connection between the function and its inverse?

Answer: The graphs are reflected over the line y = x. this swaps the x and y coordinates on each graph.

Is the connection between the function and its inverse the same regardless of how they are represented?

Answer: Yes