Learn

Practice Problem #1

Determine if the function f(x) = 2x is even, odd, or neither.

Start by substituting -x for x in the function and simplifying.

f(x) = 2x

f(-x) = 2(-x)

f(-x) = -2x

Does 2x = -2x? No

Since 2x does not equal -2x, this function is not even. For this function to be even, both expressions would have to be equivalent, or equal. You also know this function is not even because it doesn't have any even exponents.

To see if the function is odd, find the opposite of the function by multiplying it by -1 and simplifying.

f(x) = 2x

-f(x) = -(2x)

-f(x) = -2x

Is -2x = -2x? Yes

Since -2x = -2x, this function odd.

Practice Problem #2

Determine if the function is even, odd, or neither.

To determine if the function is even, substitute -x for x in the original equation and simplify.

f(x) = x2 - 4x

f(-x) = (-x)2 - 4(-x)

f(-x) = x2 + 4x

Is x2 - 4x = x2 + 4x? No

Since x² - 4 = x2 + 4x, this function is not even. For this function to be even, both expressions would have to be equivalent, or equal.

You know the function is not even, so let's check and see if it's odd. Find the opposite of the function by multiplying it by -1 and simplifying. Fill-in your signs and numbers.

f(x) = x2 - 4x

-f(x) = -1(x2 - 4x)

-f(x) = -1x2 + 4x

Does x2 + 4x? = -x2 + 4x? No

These two expressions are not equivalent, or equal, so this function is not odd.

Therefore, the function is neither even nor odd.

Helpful Hint

Most of the time, you can look at the exponents and constants to determine if the function is even or odd. Remember this information from the lesson:

If a function contains only even-numbered exponents, the function is considered an even function.

If a function contains only odd-numbered exponents and no constants, the function is an odd function.

Practice Problem #3

Which of these functions are even functions?

  1. f(x) = 3x
  2. f(x) = 4x2
  3. f(x) = 3x2 − 4
  4. f(x) = x5 − x3 − x
  5. f(x) = x6 − 4x2 − 2
  6. f(x) = −3x7

Answer: f(x) = 4x2, f(x) = 3x2 − 4, and f(x) = x6 − 4x2 − 2

Practice Problem #4

Which of these functions are odd functions?

  1. f(x) = 3x
  2. f(x) = 4x2
  3. f(x) = 3x2 − 4
  4. f(x) = x5 − x3 − x
  5. f(x) = x6 − 4x2 − 2
  6. f(x) = −3x7

Answer: f(x) = 3x, f(x) = x5 − x3 − x, and f(x) = −3x7

Practice Problem #5

Using the graph, determine if the function is odd, even, or neither.

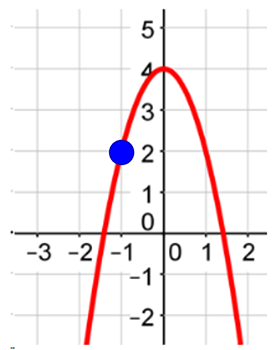
A graph of a parabola opening down with a vertex at (0, 4) with a point in blue plotted on (negative 1, 2).

To see if the function is even, pick a point on the graph. Let's pick (-1, 2). You want to see if there is a point with the same y-value, but opposite x-value. What is the opposite of -1?
Answer: 1

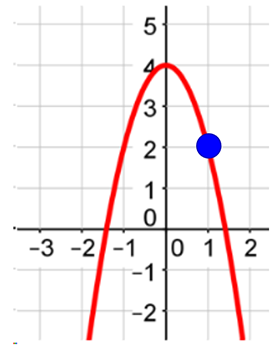
A graph of a parabola opening down with a vertex at (0, 4) with a point in blue plotted on (1, 2).

Is the point (1, 2) on the graph? Yes

Since the point (1, 2) is also on the graph, the function is even. This is true for all points on the graph. A visual check for symmetry would have also been sufficient.

Practice Problem #6

Using the graph, determine if the function is odd, even, or neither.

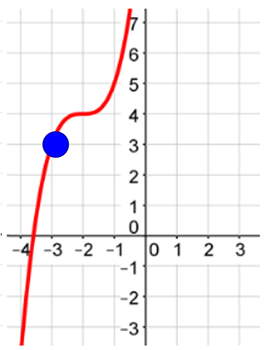
A graph of a cube function with a vertex at (negative 2, 4) with a point plotted in blue at (negative 3, 3).

To determine if the function is even, pick a point on the graph. Let's pick (-3, 3) and see if there is another point with the same y-value, but opposite x-value. What is the opposite of -3? (Keep the y-value) ( 3 , 3)

Is the point (3, 3) on the graph? No

Since the point (3, 3) is not on the graph, the function is not even. Next you will see if the function is odd.

To determine if the function is odd, pick a point on the graph. We can use (-3, 3) again. Find the opposite of this point by finding the opposite of each value. ( 3 , -3 )

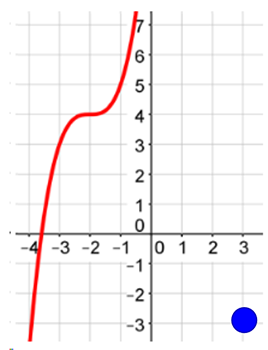
A graph of a cube function with a vertex at (negative 2, 4) with a point plotted not on the function at (3, negative 3).

Is the point (3, -3) on the graph? No

Since the point (3, -3) is not on the graph, the function is not odd. This function is neither odd nor even.