Learn
Even Odd Functions
Even Functions
Algebraically, a function is considered an even function if f(x) = f(-x) for all x's in the equation. This means that if you substitute –x for x in the original equation and get what you started with, the function is an even function.
If a function contains only even-numbered exponents, the function is considered an even function.
For example, suppose you had f(x) = x2. This doesn't have a constant but it does have an even-numbered exponent. Therefore, this is an even function.
In fact, all standard functions whose exponent is even is considered an even function. They are x4, x6, x8and so on.
Odd Function
An odd function is a function where –f(x) = f(-x). This means that if you substitute -x into the function and you get the opposite of the function, it is odd. If a function contains only odd-numbered exponents and no constants, the function is an odd function.
Suppose you have the function f(x) = x3. This does not have a constant and the exponent is odd, so this is an example of an odd function. This also holds true for f(x) = x5, x7, x9, etc.
Neither Even or Odd
What if a function is neither even nor odd?
A function will be neither even nor odd if it doesn't meet the conditions you previously learned. A function doesn't necessarily have to be even or odd because these are just names of functions.
In fact, most functions will be neither even nor odd.
This information will be important because it will give you a way to algebraically check to see if a function is even, odd, or neither. Remember:
if f(x) = f(-x), then the function is even.
if -f(x) = f(-x), then the function is odd.
Another Way of Thinking About Even Function
Another way of thinking about an even function:
Start with the statement "If f(x) = f(-x), then the function is even." This means that if you substitute -x, simplify, and you find that it is equal to the same function you began with, then the function is considered even.
Another Way of Thinking About Odd Function
Another way of thinking about an odd function:
The other statement says that "If -f(x) = f(-x), then the function is odd." This means that if you substitute -x, simplify, and you find that it is the opposite of the original function, then the function is considered odd.
Algebraic Examples
Example #1
Watch Determine Whether a Given Function is Even or Odd Given Its Equation.
Open Determine Whether a Given Function is Even or Odd Given Its Equation in a new tab
Note: The presentation may take a moment to load.
Example #2
Watch Determine Whether a Given Function is Even or Odd Given Its Equation.
Open Determine Whether a Given Function is Even or Odd Given Its Equation in a new tab
Note: The presentation may take a moment to load.
Example #3
Watch Determine Whether a Given Function is Even or Odd Given Its Equation.
Open Determine Whether a Given Function is Even or Odd Given Its Equation in a new tab
Note: The presentation may take a moment to load.
Graphic Examples
Even/Odd Graphically
You will not always be given the equation for the function. Often times, you might need to identify if a function is even or odd from its graph.
If a function is even, its graph will be symmetrical across the y-axis.
If a function is odd, its graph will be symmetrical across the origin.
Symmetrical Across the Y-Axis
You can easily identify if a graph is symmetrical across the y-axis. For example, the graphs below are all symmetrical across the y-axis.
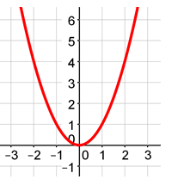
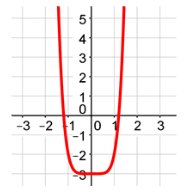
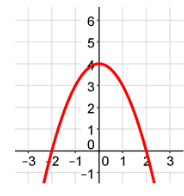
Example #4
Watch Determine Whether a Function is Symmetric across the Y-Axis Given Its Graph.
Open Determine Whether a Function is Symmetric across the Y-Axis Given Its Graph in a new tab
Note: The presentation may take a moment to load.
Symmetrical About the Origin
Each graph below is symmetrical about the origin. An easy way to tell that a graph is symmetrical about the origin is if you reflect it about one axis and then the other, it will land on top of itself.
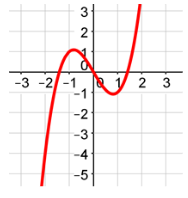
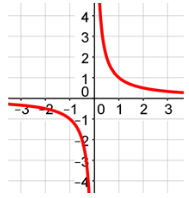
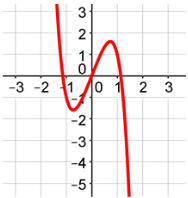
Example #5
Watch Determine Whether a Function is Symmetric about the Origin Given Its Graph.
Open Determine Whether a Function is Symmetric about the Origin Given Its Graph in a new tab
Note: The presentation may take a moment to load.
Neither Even or Odd
Now that you know how to tell if a function is even or odd based on the graph of the function, what if a graph is not a function like the ones below?
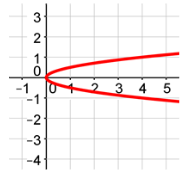
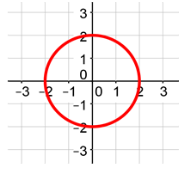
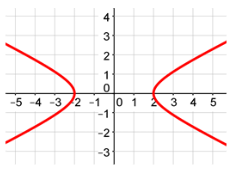
If the graph is not a function, then it is considered neither even nor odd.
Example #6
Watch Determine Whether a Function is Even, Odd, or Neither Given Its Graph.
Open Determine Whether a Function is Even, Odd, or Neither Given Its Graph in a new tab
Note: The presentation may take a moment to load.
Example #7
Watch Determine Whether a Function is Even, Odd, or Neither Given Its Graph.
Open Determine Whether a Function is Even, Odd, or Neither Given Its Graph in a new tab
Note: The presentation may take a moment to load.