Learn

Properties

The Cube Root Function

The cube root function is very similar to the radical function you learned in the last unit and behaves in much the same manner. The standard form and standard graph are below.

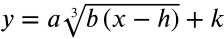
y equals a. the cube root of b times open paren x minus h close paren plus k
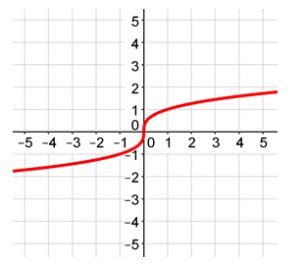
The parent graph of the cube root function is graphed. It has a vertex at (0,0) with points (negative 1, negative 1) and (1,1). The graph increases left to right.

Properties of the Cube Root Function

The vertex is (h, k). Notice that you have b(x − h) under the radical. When you state the vertex, you will write the opposite of the h-value.

y equals a. the cube root of b times open paren x minus h close paren plus k

The value of a will determine whether your graph is increasing or decreasing from left to right.

a > 0 (Positive)

The parent graph of the cube root function is graphed. It has a vertex at (0,0) with points (negative 1, negative 1) and (1,1). The graph increases left to right.

a < 0 (Negative)

The parent graph of the cube root function reflected over the x-axis is graphed. It has a vertex at (0,0) with points (negative 1, 1) and (1, negative 1). The graph decreases left to right.

The Cube Root Function

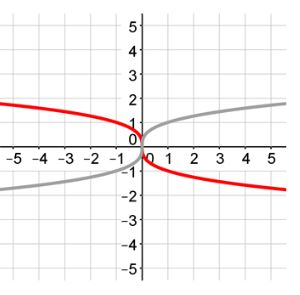
When describing how the graph has been changed, remember to use the term "reflected across the x-axis" if you have an a value which is less than zero. For example, the gray graph represents the parent graph. How was the red graph translated?

The parent graph of the cube root function is graphed in grey. It has a vertex at (0,0) with points (negative 1, negative 1) and (1,1). The graph increases left to right. The parent graph of the cube root function reflected over the x-axis is graphed in red on the same coordinate plane. It has a vertex at (0,0) with points (negative 1, 1) and (1, negative 1). The graph decreases left to right.

Examples #1, #2 and #3

Watch Determine the Vertex of a Cube Root Function Given Its Equation.

Open Determine the Vertex of a Cube Root Function Given Its Equation in a new tab

Note: The presentation may take a moment to load.

Example #4

Watch Determine the Vertex of a Cube Root Function Given Its Equation.

Open Determine the Vertex of a Cube Root Function Given Its Equation in a new tab

Note: The presentation may take a moment to load.

Example #5

Watch Determine the Vertex of a Cube Root Function Given Its Equation.

Open Determine the Vertex of a Cube Root Function Given Its Equation in a new tab

Note: The presentation may take a moment to load.

Effects of Variables

The Cube Root Function

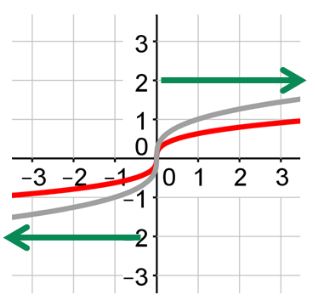
Remember, when describing how a graph has been changed, remember to use the term "reflected across the x-axis" if you have an a-value which is less than zero. For example, the gray graph represents the parent graph.

The parent graph of the cube root function is graphed in grey. It has a vertex at (0,0) with points (negative 1, negative 1) and (1,1). The graph increases left to right. The parent graph of the cube root function reflected over the x-axis is graphed in red on the same coordinate plane. It has a vertex at (0,0) with points (negative 1, 1) and (1, negative 1). The graph decreases left to right.

Effects of Variables on the Graph

The following is how each variable affects the graph.

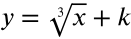y equals the cube root of x plus k The graph is shifted up.

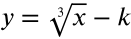y equals the cube root of x minus k The graph is shifted down.

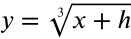y equals the cube root of x plus h The graph is shifted left.

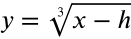y equals the cube root of x minus h The graph is shifted right.

The Value of h

Positive

If h is positive, the graph will be translated left.

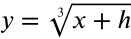
y equals the cube root of x plus h

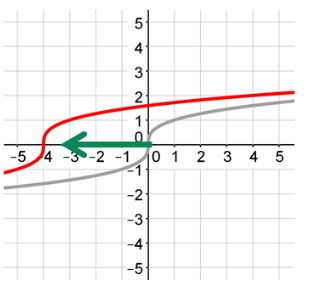
A graph of the parent graph of a cube root function in grey and a graph of a cube root function graphed in red with a vertex at (negative 4, 0). There is a green arrow showing that the red graph is translated to the left.

Negative

If h is negative, the graph will be translated right.

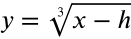
y equals the cube root of x minus h

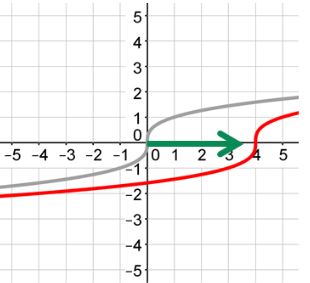
A graph of the parent graph of a cube root function in grey and a graph of a cube root function graphed in red with a vertex at (4, 0). There is a green arrow showing that the red graph is translated to the right.

The value of k

Positive

If k is positive, the graph will be translated up.

y equals the cube root of x plus k

A graph of the parent graph of a cube root function in grey and a graph of a cube root function graphed in red with a vertex at (0,4). There is a green arrow showing that the red graph is translated up.

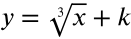
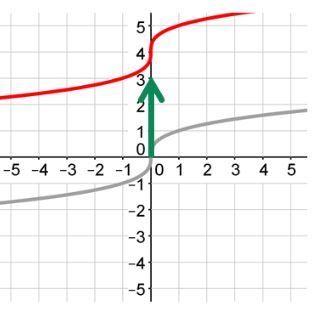
Negative

If k is negative, the graph will be translated down.

y equals the cube root of x minus k

A graph of the parent graph of a cube root function in grey and a graph of a cube root function graphed in red with a vertex at (0, negative4). There is a green arrow showing that the red graph is translated down.

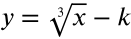
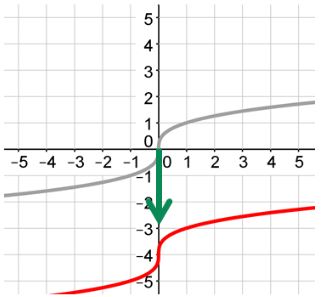
The value of a

Shrunk

If a is between 0 and 1, the graph will be shrunk vertically.

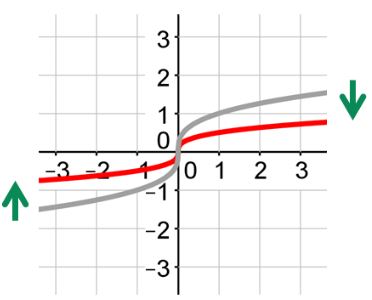
The parent graph of the cube root function is graphed in grey. It has a vertex at (0,0) with points (negative 1, negative 1) and (1,1). The graph increases left to right. On the same coordinate plane, there is a cube root function graphed in red with a vertex at (0,0) and points at approximately (negative 1, negative .4) and (1, 0.4). There are green arrows showing that the red graph is getting further away from the y-axis.

Stretched

If a is larger than 1, the graph will be stretched vertically.

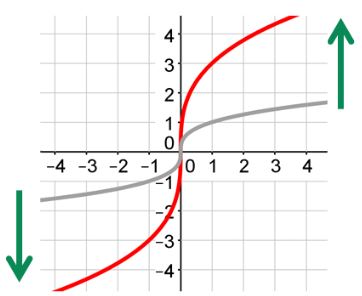
The parent graph of the cube root function is graphed in grey. It has a vertex at (0,0) with points (negative 1, negative 1) and (1,1). The graph increases left to right. On the same coordinate plane, there is a cube root function graphed in red with a vertex at (0,0) and points at (negative 1, negative 3) and (1, 3). There are green arrows showing that the red graph is getting closer to the y-axis.

The value of b

Shrunk

If b is larger than 1, the graph will be shrunk horizontally.

This will appear that the graph has been stretched vertically, but the graph is shrinking horizontally.

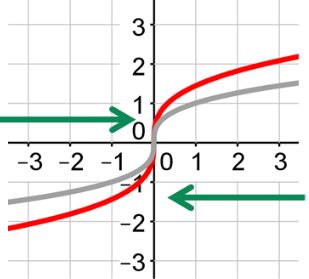
The parent graph of the cube root function is graphed in grey. It has a vertex at (0,0) with points (negative 1, negative 1.4) and (1,1.4). The graph increases left to right. On the same coordinate plane, there is a cube root function graphed in red with a vertex at (0,0) and points at approximately (negative 1, negative .4) and (1, 0.4). There are green arrows showing that the red graph is getting further away from the x-axis.

Stretched

If b is between 0 and 1, the graph will be stretched horizontally.

This graph will appear that the graph has been stretched vertically, but the graph is stretching horizontally.

The parent graph of the cube root function is graphed in grey. It has a vertex at (0,0) with points (negative 1, negative 1.4) and (1,1.4). The graph increases left to right. On the same coordinate plane, there is a cube root function graphed in red with a vertex at (0,0) and points at approximately (negative 1, negative .4) and (1, 0.4). There are green arrows showing that the red graph is getting closer to the x-axis.

Example #6

Watch Describe the Transformations of a Cube Root Function from Its Parent Graph Given Their Graphs.

Open Describe the Transformations of a Cube Root Function from Its Parent Graph Given Their Graphs in a new tab

Note: The presentation may take a moment to load.

Example #7

Watch Describe the Transformations of a Cube Root Function from Its Parent Graph Given Their Graphs.

Open Describe the Transformations of a Cube Root Function from Its Parent Graph Given Their Graphs in a new tab

Note: The presentation may take a moment to load.

Example #8

Watch Describe the Transformations of a Cube Root Function from Its Parent Graph Given Their Graphs.

Open Describe the Transformations of a Cube Root Function from Its Parent Graph Given Their Graphs in a new tab

Note: The presentation may take a moment to load.

Graphing

Graphing the Cube Root Function

To graph the cube root function, create an x-y table just as you have with other functions. You will want to start with your vertex in the middle of the table. Then, pick two values of x that are greater than the vertex and two values of x that are less than the vertex.

During this section, you will need a scientific calculator. If you do not have a scientific calculator, use this online calculator.

Example #9

Watch Graph a Cube Root Function.

Open Graph a Cube Root Function in a new tab

Note: The presentation may take a moment to load.

Example #10

Watch Graph a Cube Root Function.

Open Graph a Cube Root Function in a new tab

Note: The presentation may take a moment to load.