Introduction
You have learned the effects of the a, h, and k on the graphs of absolute value, quadratic, and square root functions. In this lesson, you will be introduced to the b of an equation and study the effects of the b on the graph. You are also going to study the cube root function. This function looks like an S that has been stretched out.
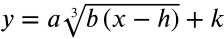
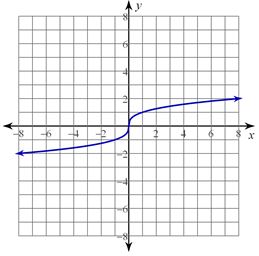
You have learned if a is negative that the graph is reflected over the x-axis. If the b is negative, then the graph is reflected over the y-axis.
The graph goes forever left and right, so the domain will have no restrictions. The domain is always All Real Numbers or (−∞,∞). The graph goes up and down forever, so the range is also All Real Numbers or (−∞,∞).
Following successful completion of this lesson, students will be able to...
- Graph functions expressed symbolically, and show key features of the graph, by hand in simple cases and using technology for more complicated cases.
- Graph cube root functions.
- Identify the effect on the graph of replacing f(x) by f(x) + k, k f(x), f(kx), and f(x + k) for specific values of k (both positive and negative); find the value of k given the graphs. Experiment with cases and illustrate an explanation of the effects on the graph using technology.
Enduring Understandings
- Graphs are visual representations of solution sets of equations and inequalities.
- There is a root that corresponds to every power.
- Radical expressions may be combined using Properties of Real Numbers.
- Characteristics of radical and rational exponent expression as well as their representations are useful in solving real-world problems.
The above objectives correspond with the Alabama Course of Study: Algebra II with Statistics standards: 30a and 34.