Learn

Translating Radical Functions

The equation of the standard form of a radical function is 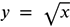y equals the square root of x

To translate the graph of the function, you will study the vertex form of a radical function which is 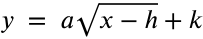y equals a. the square root of x minus h plus k

In this form, (h, k) represents the vertex of the function and will tell you how the graph is translated. The value of a will tell you how the graph opens.

Notice the vertex of the function is (h, k). The expression under the radical is x - h, so you will determine the opposite of the h when stating the vertex.

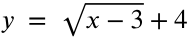
y equals the square root of x minus 3 plus 4

In the function above, the vertex would be (3, 4) because the value of h is the opposite of −3 which is 3 and the value of k is 4.

Examples #1 and #2

Watch Find the Vertex of a Radical Function Given Its Equation.

Open Find the Vertex of a Radical Function Given Its Equation in a new tab

Note: The presentation may take a moment to load.

Translating the Parent Graph

The vertex will tell you how the graph of the function is translated from the parent graph.

How is the function below translated from 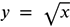y equals the square root of x

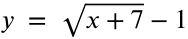
y equals the square root of x plus 7 minus 1

The vertex for this function is at (−7, −1). This means the graph is translated seven units left and one unit down.

Examples #3 and #4

Watch Describe the Translation of a Radical Function from Its Parent Graph Given Its Equation.

Open Describe the Translation of a Radical Function from Its Parent Graph Given Its Equation in a new tab

Note: The presentation may take a moment to load.

Example #5

Watch Describe the Translation of a Radical Function from Its Parent Graph Given Its Graph.

Open Describe the Translation of a Radical Function from Its Parent Graph Given Its Graph in a new tab

Note: The presentation may take a moment to load.

The importance of a

When referring back to the vertex form of a radical function, the value of a will determine whether your graph will open up or down. The value of a also effects the steepness of the graph.

Open Up or Down?

Given the equation 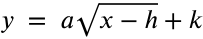y equals a. the square root of x minus h plus k , you can easily determine if the graph will open up or down. Consider the two cases below.

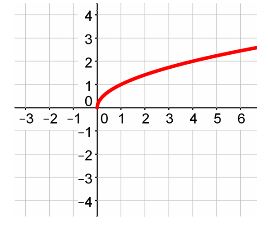
The parent graph of the square root function is graphed on a coordinate plane with a vertex at (0,0) and passes through the following points: (1, 1) and (4,2) . The graph goes up and to the right.
a > 0
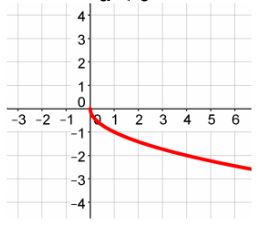
The parent graph of the square root function reflected over the x-axis is graphed on a coordinate plane with a vertex at (0,0) and passes through the following points: (1, negative 1) and (4, negative 2) . The graph goes down and to the right.
a < 0

Examples #6 and #7

Watch Describe Key Features of a Radical Function Given Its Equation.

Open Describe Key Features of a Radical Function Given Its Equation in a new tab

Note: The presentation may take a moment to load.

Stretching and Shrinking

You can easily identify stretching and shrinking on a graph. The red and purple graphs below have been stretched and the blue graph was shrunk. Notice the values of a.

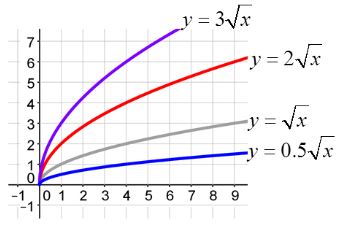
A coordinate plane with 4 square root functions graphed all having a vertex at (0,0) and going up and to the right. The closest graph to the y-axis is y = 3 times the square root of x. The next closest to the y-axis is y = 2 times the square root of x. The next closest to the y-axis is y = the square root of x. The graph that is the farthest from the y-axis is y = 0.5 times the square root of x.

Example #8 Graphing

Watch Graph a Radical Function and Describe Its Translation from the Parent Graph.

Open Graph a Radical Function and Describe Its Translation from the Parent Graph in a new tab

Note: The presentation may take a moment to load.

Example #9

Watch Graph a Radical Function and Describe Its Translation from the Parent Graph.

Open Graph a Radical Function and Describe Its Translation from the Parent Graph in a new tab

Note: The presentation may take a moment to load.