Introduction
In the last lesson, you learned to graph radical functions by creating an x-y table and plotting points. You will apply some of that knowledge in this lesson as well as how the graph was translated from the parent graph. Remember that a parent graph is the graph of a function in standard form. For example, the standard form of a radical function is 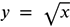 and the parent graph is shown below. Parent graphs will always have (0, 0) as a point on the graph and most commonly as the vertex.
and the parent graph is shown below. Parent graphs will always have (0, 0) as a point on the graph and most commonly as the vertex.
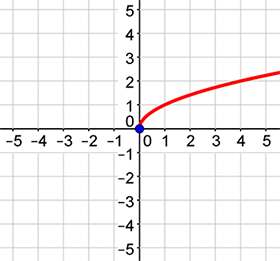
Before beginning the lesson, use GeoGebra - Translating Radical Functions to answer the following questions. Post your answers to the 5.03 Radical Functions Discussion.
Respond to at least one other student, telling them any differences that you saw between the answers that they posted and the answers that you posted. Together, the two of you should agree on an answer.
Questions to answer:
- What does the value of h control?
- What does the value of k control?
- What does the value of a control?
- If h = 0 and k = 0, which way does the graph open when a > 0 (Positive)?
- If h = 0 and k = 0, which way does the graph open when a < 0 (Negative)?
- If h = 1 and k = 2, what are the coordinates of the blue point?
- If h = −3 and k = −2, what are the coordinates of the blue point?
Following successful completion of this lesson, students will be able to...
- Relate the domain of a function to its graph and, where applicable, to the quantitative relationship it describes.
- Graph functions expressed symbolically, and show key features of the graph, by hand in simple cases and using technology for more complicated cases.
- Graph square root functions.
Enduring Understandings
- Graphs are visual representations of solution sets of equations and inequalities.
- Graphs of functions that are inverses of each other are reflections across the line y = x.
- There is a root that corresponds to every power.
- Radical expressions may be combined using Properties of Real Numbers.
- Characteristics of radical and rational exponent expression as well as their representations are useful in solving real-world problems.
The above objectives correspond with the Alabama Course of Study: Algebra II with Statistics standards: 29 and 30