Learn

Practice Problem #1

Determine the domain of the function 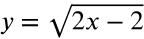y equals the square root of 2 x minus 2

Take the expression under the radical and set it greater than or equal to zero and solve.

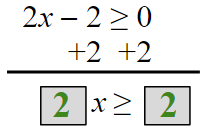
2x minus is greater or equal to 0. Add 2 to both sides , then you have 2x is greater or equal to 2.


Continue to solve the problem.

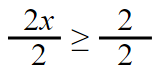
2 x over 2 is greater than or equal to two halves

x ≥ 1

Practice Problem #2

Determine the domain of the function 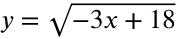y equals the square root of negative 3 x plus 18

Set the expression under the radical greater than or equal to zero and solve.

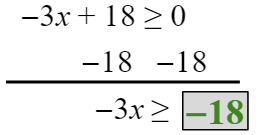
Negative 3x plus 18 is greater equal to 0. Subtract 18 from both sides, then you have negative 3x is greater or equal to negative 18.

Continue to solve the inequality. Remember to flip your sign.

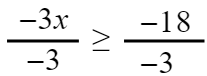
negative 3 x over negative 3 is greater than or equal to negative 18 over negative 3

x ≤ 6

Practice Problem #3

Graph the function 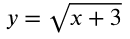y equals the square root of x plus 3

Which of the following is the domain of the function? x ≥ -3

The domain for this function is all values of x that are greater than or equal to -3. Therefore, choose values of x accordingly.

x y Instructions
−3 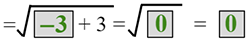equals the square root of negative 3 plus 3 equals the square root of 0 equals 0 Substitute x = −3 and simplify to find y.
−2 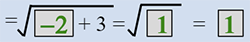equals the square root of negative 2 plus 3 equals the square root of 1 equals the square root of 1 Substitute x = −2 and simplify to find y.
1 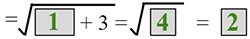equals the square root of 1 plus 3 equals the square root of 4 equals the square root of 2 Substitute x = 1 and simplify to find y.
6 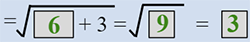equals the square root of 6 plus 3 equals the square root of 9 equals the square root of 3 Substitute x = 6 and simplify to find y.

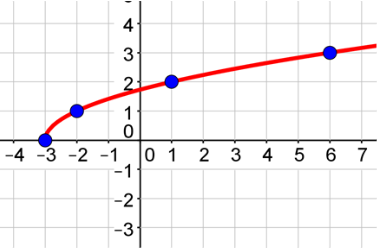
Plot your points.

x y
-3 0
-2 1
1 -2
6 3
The following points are plotted on a coordinate plane: (negative 3,0), (negative 2, 1), (1,2), and (6,3).

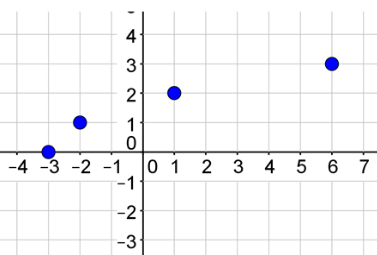
Draw your graph.

The graph of a square root function is graphed on a coordinate plane with a vertex at (negative 3,0) and passes through the following points: (negative 2, 1), (1,2), and (6,3). The graph is going up and to the right.

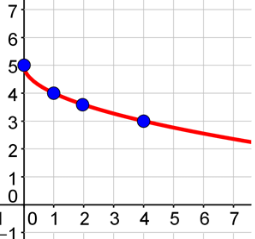
Practice Problem #4

Graph the function 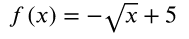f of x equals the negative square root of x plus 5

The domain of this function is x ≥ 0, so you will pick values of x which are greater than 0.

x y Instructions
0 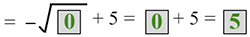equals the negative square root of 0 plus 5 equals 0 plus 5 equals 5 Substitute x = 0 and solve for y.
q 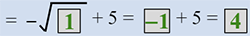equals the negative square root of 1 plus 5 equals negative 1 plus 5 equals 4 Substitute x = 1 and solve for y.
2 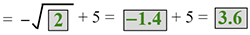equals the negative square root of 2 plus 5 equals negative 1.4 plus 5 equals 3.6 Substitute x = 2 and solve for y. You will get a decimal.
4 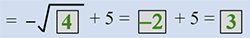equals the negative square root of 4 plus 5 equals negative 2 plus 5 equals 3 Substitute x = 4 and solve for y.

Plot your points.

x y
0 5
1 4
2 3.6
4 3

The following points are plotted on a coordinate plane: (0,5), (1,4), (2, 3.6), and (4,3).

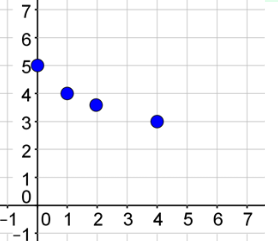
Draw your graph.

The graph of a square root function is graphed on a coordinate plane with a vertex at (0,5) and passes through the following points: (1,4), (2, 3.6), and (4,3). The graph is going down and to the right.