Learn

Domain

Domain of a Radical Function

Until this time, you haven't had to worry about the domain of a function. Recall that the domain of a function is the possible x-values of the function.

In this lesson, the domain is going to be important because you cannot determine the square root of a negative value and get a real answer.

Determine the Domain

Determine the domain of 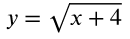y equals the square root of x plus 4

To determine the domain, you will take the radicand and set it to be greater than or equal to zero.

x + 4 ≥ 0

Why use greater than or equal to zero?

You will set the expression to be greater than or equal to zero because you do not want a negative number. You want 0 and any positive number. You cannot take a square root of a negative number in the real number system.

Solve to determine your domain.

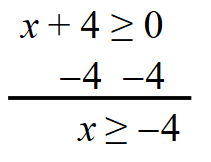
x plus 4 is greater or equal to 0. Subtract 4 from each side. X is greater or equal to negative 4

This means that your domain is all values that are greater than or equal to −4. Anything less than −4 does not work with this function because it will give you a negative value.

Example #1

Watch Determine the Domain of a Radical Function.

Open Determine the Domain of a Radical Function in a new tab

Note: The presentation may take a moment to load.

Graphing

Radical Functions

Radical functions are functions which contain a radical, or square root. The graph will look like half of a parabola turned sideways. Your graphs will look like any of the four graphs below.

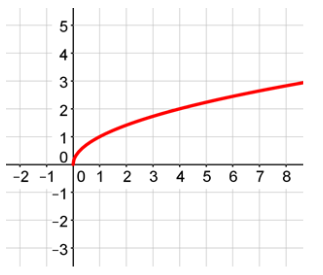
A graph of a square root function. The vertex is at (0,0) and has points at (1,1), (4,2) with a curve going through them going up and right.
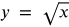
y equals the square root of x
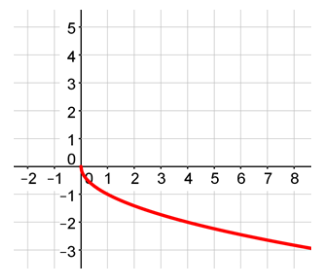
A graph of a square root function. The vertex is at (0,0) and has points at (1, negative 1), (4, negative 2) with a curve going through them going down and right.
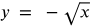
y equals the negative square root of x
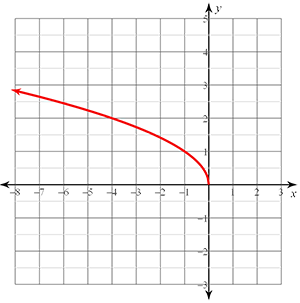
A graph of a square root function. The vertex is at (0,0) and has points at (negative 1, 1), (negative 4, 2) with a curve going through them going up and left.
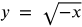
y equals the square root of negative x
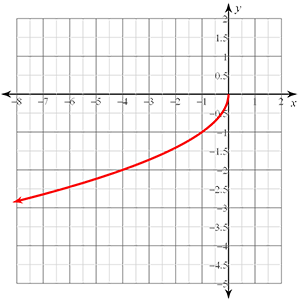
A graph of a square root function. The vertex is at (0,0) and has points at (negative 1, negative 1), (negative 4, negative 2) with a curve going through them going down and left.
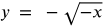
y equals the negative square root of negative x

Example #2

Watch Graph Radical Functions.

Open Graph Radical Functions in a new tab

Note: The presentation may take a moment to load.

Example #3

Watch Graph Radical Functions.

Open Graph Radical Functions in a new tab

Note: The presentation may take a moment to load.

Example #4

Watch Graph Radical Functions.

Open Graph Radical Functions in a new tab

Note: The presentation may take a moment to load.

Example #5

Watch Graph Radical Functions.

Open Graph Radical Functions in a new tab

Note: The presentation may take a moment to load.