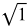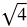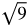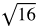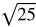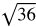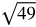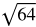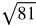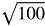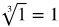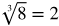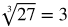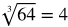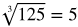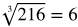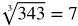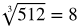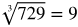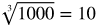Learn
Power and Root
You might want to recall the list of perfect square and cube roots while working through this lesson.
Perfect square roots:
Perfect cubed roots:
Rational Exponents
A rational exponent can be rewritten as a radical. The numerator of the rational exponent will be the power of the radicand The radicand is the number under the radical. and the denominator will be the index The index is the type of root: square root or cube root .
You can also think of the rational exponent as power divided by the root.
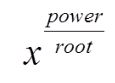
Example #1
Identify the power and root for the rational exponent.
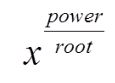

The power will be 6 and the root will be 2.
This can be rewritten as 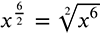 .
.
Power = 6, root = 2
Example #2
Identify the power and root for the rational exponent.

The power of the rational exponent is 3 and the root is 2.
Rewrite using radical notation.
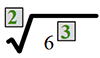
Simplify 63 under the radical.
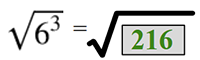
Simplify the radical by rewriting 216 as the product of a perfect square and the remainder.
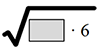
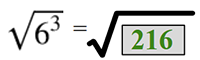 =
= 

=
Example #3
Identify the power and root for the rational exponent.
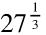
Begin by writing the expression using radical notation.
What is the power?
What is the root?
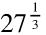 =
= 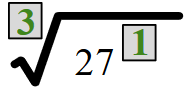
Simplify the radical.
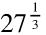 =
= 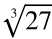 =
=
Example #4
Watch Rewrite Radicals in Exponential Form.
Open Rewrite Radicals in Exponential Form in a new tab
Note: The presentation may take a moment to load.
Example #5
Rewrite the radical using exponential notation.
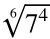
What is the power?
What is the root?
Using the notation 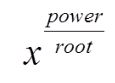 , complete the expression.
, complete the expression.
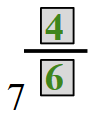
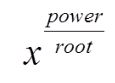 =
= 
Simplify the rational exponent.
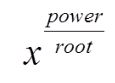 =
=  =
= 
Example #6
Watch Simplify Rational Exponents by Rewriting in Radical Form.
Open Simplify Rational Exponents by Rewriting in Radical Form in a new tab
Note: The presentation may take a moment to load.
Rules of Exponents
Reviewing the Exponent Rules
Earlier in this course, you learned how to apply the properties of exponents. Review each of the following:
Product Rule of Exponents
35 x 32 = 35 + 2 = 37 = 2187
Power of a Power Rule of Exponents
(35)2 = 35(2) = 310 = 59049
Quotient Rule of Exponents
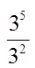 = 35 - 2 = 33 = 27
= 35 - 2 = 33 = 27
Example #7
Watch Apply Properties of Exponents to Simplify Expressions.
Open Apply Properties of Exponents to Simplify Expressions in a new tab
Note: The presentation may take a moment to load.
Methods
When you are simplifying rational exponents, you can rewrite in radical notation to simplify or you can apply the properties of exponents to simplify.
Example #8
Watch Apply Properties of Exponents to Simplify Expressions.
Open Apply Properties of Exponents to Simplify Expressions in a new tab
Note: The presentation may take a moment to load.