Introduction
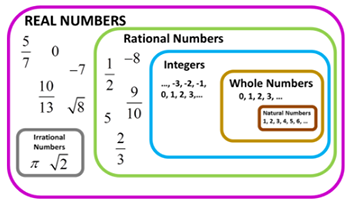
Recall that a rational number is a number which can be written as a fraction. Therefore, basically all numbers in the universe of numbers except for irrational numbers are considered rational. You can see from the picture below that rational numbers include the integers, whole numbers, and natural numbers.
Suppose you had 22. This can also be written as 
, which makes it a rational exponent.
In this lesson, you will explore rational expressions and learn how to re-write base numbers and exponents as radicals.
Following successful completion of this lesson, students will be able to...
- Interpret expressions that represent a quantity in terms of its context.
- Write a function defined by an expression in different but equivalent forms to reveal and explain different properties of the function.
Enduring Understandings
- A basis for the complex numbers is a number whose square is −1.
- Every quadratic equation has complex number solutions.
- There is a root that corresponds to every power.
- Radical expressions may be combined using Properties of Real Numbers.
- Characteristics of radical and rational exponent expression as well as their representations are useful in solving real-world problems.
The above objectives correspond with the Alabama Course of Study: Algebra II with Statistics standards: 12 and 31.