Try It
Practice Problem #1
The polynomial function P(x) = x4 + 4x3 - 3x2 - 18x crosses the x-axis at ___
Answer: You should be able to factor out an x immediately. x (x3 + 4x2 - 3x - 18) From here, you can use the rational roots theorem to find that the possible roots are the factors of 18. Substitute these into the polynomial in parentheses to see what gives you a zero. x = 0, -3, 2
P(x) = x4 + 4x3 - 3x2 - 18x The x-coordinate(s) of the relative maximum and/or relative minimum points are.___
Answer: Remember, the zeroes are x = -3, 0, and 2. The relative minimums will occur halfway between each set of points. The midpoint between -3 and 0 -3/2. The midpoint betwen 0 and 2 is 1. So the answers are -3/2 and 1.
P(x) = x4 + 4x3 - 3x2 - 18x The coordinates of the relative maximum and/or minimum points are__
Answer: 
P(x) = x4 + 4x3 - 3x2 - 18x crosses the x-axis at___
We already know that the relative minimum and maxium points are at 1 and -3/2. Substitute these values in for x to find the coordinates for the points.
([-3/2], 11[13/16]), (1, -16)
4) What is the graph of the function P(x) = x4 + 4x3 - 3x2 - 18x?
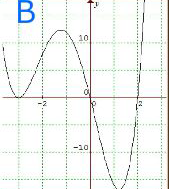
We can determine this soley with our understanding of the x intercepts. Graphs A and D do not have an x intercept at 0, so we can eliminate them. Graph C does not have an x interecept at -3, so it is out as well. Using what we know, we can tell that B is the correct graph.
Practice Problem #2
The polynomial function P(x) = x + x - 10x + 8 crosses the x-axis at___
Answer: Because this equation has degree of 3, it should have 3 roots. We can use the rational roots theorem to determine that the possible roots are the factors of 8. Then, substitute them into the polynomial to find our zeroes. so x = -4, 1, 2
P(x) = x3 + x2 - 10x + 8 The x-coordinate(s) of the relative maximum and/or relative minimum points are____
Answer: Again, we already know that the x-interepts are at -4, 1, and 2. The relative minumum and maximum points accur halfway between these points. Midpoint -4 and 1 = (-4 + 1)/2 = -3/2 Midpoint 1 and 2 = (1 + 2)/2 = 3/2
P(x) = x3 + x2 - 10x + 8 The coordinates of the relative maximum and/or minimum points are___
Answer: 
We already know that the relative minium and maximum points are at 3/2 and -3/2/. Substitute these values in for x to find the coordinates for the points.
What is the graph of the function P(x) = x + x - 10 + 8?
Answer: We can determine this solely with our understanding of the x-intercepts. Graphs C and D do not have an x-intercept at -4, so we can eliminate them. Graph B has only negative roots, so it is out as well. Using what we know, we can tell that A is the correct graph.
