Learn

Sketching Graphs

Steps to Sketch a Graph of a Polynomial

  • Step 1 Find the x-intercepts: set each factor equal to zero and solve.
  • Step 2 Mark each x-intercept on the x-axis. Do not number the y-axis.
  • Step 3 Find the relative maximum and/or the relative minimum between each x-intercept.
  • Step 4 Sketch the graph.

Example #1

Watch Sketch the Graph of a Polynomial Function.

Open Sketch the Graph of a Polynomial Function in a new window

Note: The presentation may take a moment to load.

Example #2

Watch Sketch the Graph of a Polynomial Function.

Open Sketch the Graph of a Polynomial Function in a new window

Note: The presentation may take a moment to load.

Steps for Finding Rational Roots and/or Factors

Here are the steps for finding Rational Roots and/or Factors, Graphs:

  1. Write all the factors of the first and last terms of the polynomial.
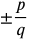
  2. Write all the possible rational roots by making fractions where the numerator is a factor of the last term and the denominator is a factor of the first term, plus or minus p over q
  3. List P (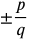plus or minus p over q) in order from smallest to largest.
  4. Evaluate all.
  5. Choose zeros/roots.
  6. Write factors (when asked to).
  7. Graph (when asked to).

Example #3

Watch Sketch the Graph of a Polynomial Function.

Open Sketch the Graph of a Polynomial Function in a new window

Note: The presentation may take a moment to load.

Use a Graphing Tool

So far, we have found the roots of polynomial functions or equations by using the Remainder Theorem or by using synthetic division. However, these methods only work when our roots are rational.

What do we do when we can't find the roots using these methods but we can clearly see a graph crosses the x-axis (in other words, has real roots)?

If the roots of a polynomial function or equation are irrational, we will need the help of a graphing utility. We might use our graphing calculator or we might use a computer program such as Geogebra to help us find the roots. Let's start by using a graphing calculator.

Example #4

Calculator

Watch Find the Roots of a Polynomial Function Using a Graphing Tool.

Open Find the Roots of a Polynomial Function Using a Graphing Tool 1 in a new window

Note: The presentation may take a moment to load.

GeoGebra

Open Find the Roots of a Polynomial Function Using a Graphing Tool 2 in a new window

Note: The presentation may take a moment to load.

Example #5

Sketch the graph of f(x) = 2x3 − x2 − 15x − 10

First, how many solutions do we expect to find?

Hint: It is the leading degree.

Answer: 3

At most, how many x-intercepts do we expect to have?

Hint: It is the same as the leading degree.

Answer: 3

At most, how many turning points do we expect to have?

Hint: 1 less than the leading degree.

Answer: 2

What will the end behavior be for this graph? Starts ___blank and ends ___blank.

Hint: It is a positive odd function.

Answer: Starts down and ends up.

Now, first look to see if this will factor.

It will not factor. You can try to factor by grouping, but it will not work. So, we need to find the factors of our p and q now.

Factors of 10: ±1, ±2, ±5, ±10

Factors of 2: ±1, ±2

Example #5 List Combinations

List all combinations of the factors of 10 divided by the factors of 2 ±1, plus or minus one-half, ±2, ±5, plus or minus five over two, ±10


Now, list them in order from least to greatest and evaluate.

  • f(− 10) = − 1960
  • f(− 5) = − 210
  • f(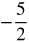negative five over two) = − 10
  • f(− 2) = 0
  • f(− 1) = 2
  • f(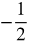negative one-half) = − 3
  • f(one-half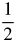) = − 17.5
  • f(1) = − 24
  • f(2) = − 28
  • f(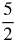) = −22.5
  • f(5) = 140
  • f(10) = 1740

x = −2 is the only rational solution. The other two solutions will be either be either irrational or imaginary.

Example #5 Use Synthetic Division

We are missing 2 solutions. They will either be irrational or imaginary. We can use synthetic division using −2 to find the other solutions.

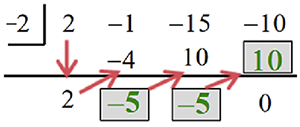
the number negative 2 in a box to the left right. On the right side of the box in row 1 is 2, negative 1, negative 15, negative 10. On the second row, there is a negative 4 below the negative 1 in row 1. There is a horizontal line below row 2. Below the line, there is a 2 below the 2 in row 1 with an arrow pointing down to indicate to bring the 2 down. There is an arrow coming from the 2 on row 3 pointing to the negative 4 on row 2 and there is a negative 5 below negative 4 and an arrow coming from negative 5 pointing to the 10 on row 2. There is a negative 5 below the 10 on row 2 with an arrow pointing toward a 10 at the end of row 2 and a 0 below it on row 3.

Example #5 Use the Quadratic Equation

We will find the other solutions by solving this equation.

2x2 − 5x − 5 = 0

Since this is a quadratic formula, we can solve it by using the quadratic equation. Identify the a, b, and c.

  • a = 2
  • b = −5
  • c = −5

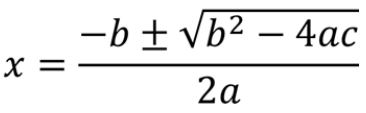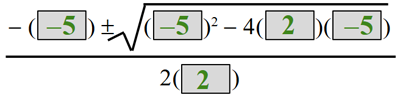
x equals the fraction with numerator negative b plus or minus the square root of b squared minus four times a times c and denominator two a = the fraction with numerator negative negative 5 plus or minus the square root of open paren negative 5 close paren squared minus 4 times open paren the square root of 2 close paren times negative 5 and denominator 2 times 2

the fraction with numerator 5 plus or minus the square root of 25 plus 40 and denominator 4 = the fraction with numerator five plus or minus the square root of sixty-five and denominator 4.

The zeros of this function are −2, the fraction with numerator five plus or minus the square root of sixty-five and denominator 4.


Example #5 Find Points

To find points between the three x-intercepts, we need to find the decimals of the two irrational zeros.

the fraction with numerator five plus the square root of sixty-five and denominator 4. ≈ 3.27.

the fraction with numerator five minus the square root of sixty-five and denominator 4. ≈ −0.77

To find a point halfway between −0.77 and −2, add them and divide by 2. We get −1.39. Next, find f(–1.39).

f(–1.39) = 2(−1.39)3 − (−1.39)2 − 15(−1.39) − 10 = 3.55 (−1.39, 3.55) is a point between −0.77 and −2.

Find a point halfway between –0.77 and 3.27. It will be 1.25. Find f(1.25).

f(1.25) = 2(1.25)3−(1.25)2 − 15(1.25) − 10 = −26.41

(1.25, −26.41) is a point between −.077 and 3.27.

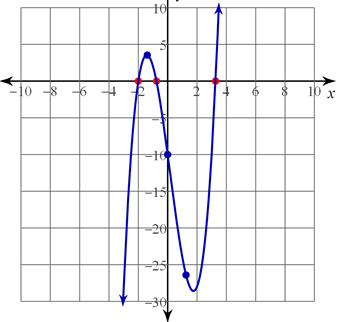
  1. (−1.39, 3.55) is a point between −0.77 and −2.
  2. (1.25, −26.41) is a point between −0.77 and 3.27.
    • We can find the y-intercept by putting 0 in for x.
    • 2(0)3 − (0)2 − 15(0) − 10 = −10
    • The y-intercept is −10.

Example #5 Complete the Graph

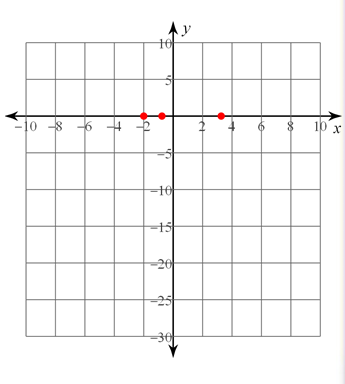
A coordinate plane with points on the x-axis at negative 2, negative 0.77, and 3.27.
  1. Let's begin by plotting our x-intercepts
    • Next, we can plot our other points that we found and the y-intercept.
    • (−1.39, 3.55)
    • (1.25, −26.41)
    • The y-intercept is −10.
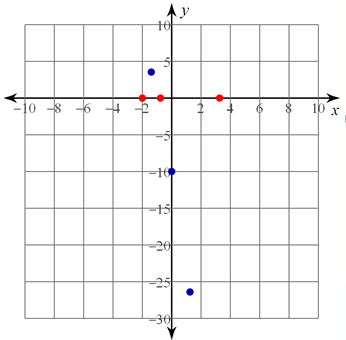
A coordinate plane with points on the x-axis at negative 2, negative 0.77, and 3.27 and points at (negative 1.39, 3.55), (0, negative 10), and (1.25, negative 26.41).

We stated in the beginning that this is a positive odd function, so the graph will start down and end up. We can now draw the curve through the points to complete the graph.

A coordinate plane with a polynomial that starts down and ends up passing through the points (negative 2,0), (negative 1.39, 3.55), (negative 0.77,0), (0, negative 10), (negative 1.39, 3.55), and (3.27,0).