Learn

Rational Roots

Rational Roots Theorem

Let's look at this quadratic equation: P(x) = 2x2 + 7x + 6. We cannot just say the factors are (x + 6) and (x + 1) because there is a coefficient on the leading term. The leading coefficient changes the process in order to obtain the factors of this equation. The factors for this are (2x + 3)(x + 2) and the zeros are negative 3 over 2 comma negative 2

Notice that the product of the first term of each factor, 2x and x, gives us the first term, 2x2, and that the product of the constant terms in each fact, 3 and 2, gives us the constant term in the polynomial, 6.

This leads us to the Rational Roots Theorem. Notice this is for rational roots. Some of the roots may be irrational or imaginary and we will look at them as well.

Rational: A number of the form a/b where a and b are both integers and b is not equal to zero.

Irrational: Not rational. Nondetermining, non-repeating decimals. Usually include radicals or π.

Imaginary: Those numbers that contain i, the square root of a negative number.


The Rational Roots Theorem:

For any polynomial, P(x), where all coefficients are integers, every rational root/zero will be of the form p over q where p is a factor of the constant term and q is a factor of the lead coefficient.

The Rational Roots Theorem gives us the possible rational roots. If we combine this with the Factor Theorem, we can then find the actual rational roots.

Steps

Steps for finding Rational Roots and/or Factors, Graphs

Axn + Bxn − 1 + Cxn − 2 ... + Cx + E

  1. Write all the factors of the first and last terms of the polynomial.
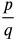
  2. Write all the possible rational roots by making fractions where the numerator is a factor of the last term and the denominator is a factor of the first term. ± p over q
  3. List P(± 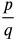p over q) in order from smallest to largest.
  4. Evaluate all.
  5. Choose zeros/roots
  6. Write factors (when asked to)
  7. Graph (when asked to)

You should copy these steps into your notebook. Note that steps 6 and 7 may not be called in for every problem.

Example #2

Open Apply the Rational Roots and Factor Theorems to Find Rational Roots and Factors of a Polynomial Function in a new window

Note: The presentation may take a moment to load.

Example #3

Open Apply the Rational Roots and Factor Theorems to Find Rational Roots and Factors of a Polynomial Function in a new window

Note: The presentation may take a moment to load.

Example #4

Create a polynomial of third degree with one positive, two negative real rational zeros.


We should recognize immediately that we will have three factors. For a positive root we could use x = 1. For the two negative roots, we could use x = −2 and x = −3. (You really could use any numbers fitting the criteria here. We are trying to pick numbers that will be easy to multiply.)

x = −3


x = −2

x = 1

Now make factors.

Factors are: (x + 3)(x + 2)(x − 1)

Now, multiply these factors together. Start with the first two.

(x2 + 5)(x − x2 + 6)(x − 1)

Now, finish multiplying.

x3 + 5x2 + 6x − x2 − 5x − 6

x3 + 4x2 + x − 6

Note: This is only one example of many that will fit the description requested.

Example #5

Open Find All the Roots of a Polynomial Function in a new window

Note: The presentation may take a moment to load.