Try It
Practice Problems
Practice Problem #1
Tell the end behavior of the following function:
f(x) = −3x3 + 2x + 1
What is the leading coefficient?
Answer: −3x3
Is the degree even or odd?
Answer: odd
Is the leading coefficient positive or negative?
Answer: negative
A negative odd function starts _______blank and ends ________blank.
Answer: A negative odd function starts up and ends down.
As x → ___blank, f(x) → ___blank.
As x → ___blank, f(x) → ___blank.
Answer:
As x →− ∞, f(x) → ∞.
As x → ∞, f(x) → −∞.
Practice Problem #2
Look at the graph and describe the end behavior.
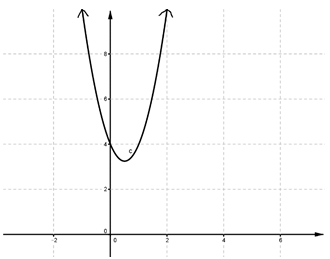
Answer:
x → −∞, f(x) → ∞, x → ∞, f(x) → ∞.
Practice Problem #3
Look at the graph and describe the end behavior.
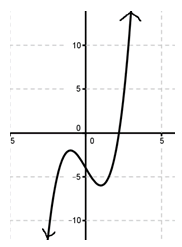
Answer:
x → −∞, f(x) → −∞, x → ∞, f(x) → ∞.
Practice Problem #4
Look at the graph and describe the end behavior.
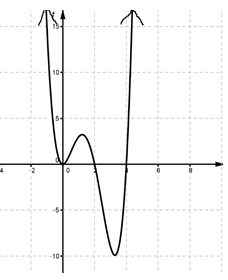
Answer:
x → −∞, f(x) → ∞, x → ∞, f(x) → ∞.
Practice Problem #5
Look at the graph and describe the end behavior.
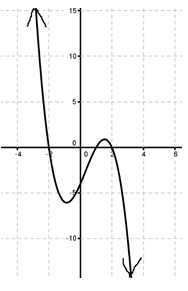
Answer:
x → −∞, f(x) → ∞, x → ∞, f(x) → −∞.
Practice Problem #6
Look at the graph and determine the number of turning points. Which answer is correct?
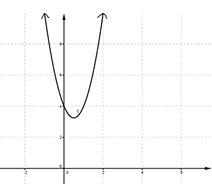
Answer: 1
Practice Problem #7
Look at the graph and determine the number of x-intercepts. Which answer is correct?

Answer: 0
Practice Problem #8
Look at the graph and determine the number of x-intercepts. Which answer is correct?

Answer: 3
Practice Problem #9
Look at the given function and determine the end behavior.
f(x) = 4x2 + x − 2
Answer:
x → −∞, f(x) → ∞, x → ∞, f(x) → ∞.
Practice Problem #10
Look at the given function and determine the maximum of x-intercepts.
f(x) = 4x2 + x − 2
Answer: 2
Practice Problem #11
Look at the given function and determine the maximum of turning points.
f(x) = 4x2 + x − 2
Answer: 1
Practice Problem #12
Look at the given function and determine the maximum of turning points.
f(x) = 4x2 + 6x 4 + x5 + 7
Answer: 5