Learn
Practice Problems
Practice Problem #1
The daily profit, P, of a cotton candy vendor at the fair is described by the function P = −60x2+ 240x − 80, where x dollars is the selling price of a bag of cotton candy. Use this equation to answer the questions below.
- What is the maximum daily profit?
- How much should each bag of cotton candy cost to generate the maximum profit?
- How much profit would be generated if the cotton candy sold for $1.50?
1. What is the maximum daily profit?
To find the maximum daily profit, you will want to find the maximum point of the function.
Hint: The maximum point is also the vertex.
![]() =
= 
Simplify
![]() =
=
Substitute x = 2 into the equation and simplify.
P = −60x2+ 240x − 80
P = −60(___blank)2+ 240(___blank) − 80
Answer: 2, 2
P = −60(4) + 480 − 80
P = −240 + 480 − 80
P = $ ___blank
Answer: 160
So, P = 160 when x = 2. This means the maximum profit will be $160.
2. How much should each bag of cotton candy cost to generate the maximum profit?
You found that P = 160 (the maximum profit) when x = 2. If the x-axis represents the cost per bag, what should the price of each bag be to have the maximum profit?
Cost = $ ___blank per bag
Answer: 2
3. How much profit would be generated if the cotton candy sold for $1.50?
Remember the x-axis represents the cost per bag. Therefore, substitute x = $1.50 and simplify to find P, the profit.
Substitute x = $1.50 into the original equation.
P = −60x2+ 240x − 80
P = −60(___blank)2+ 240(___blank)− 80
Answer: 1.50, 1.50
P = −60( ___blank ) +___blank − 80
Answer: 2.25, 360
P = ___blank
Answer: 145
1. What is the maximum daily profit? $160
2. How much should each bag of cotton candy cost to generate the maximum profit? $2
3. How much profit would be generated if the cotton candy sold for $1.50? $145
Practice Problem #2
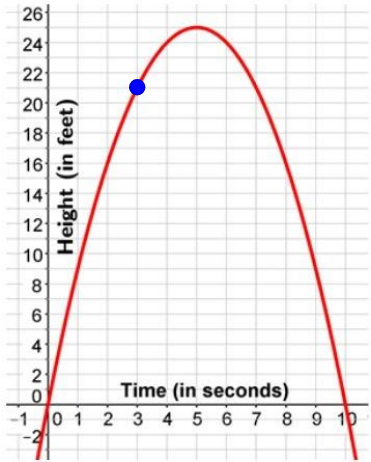
A ball is thrown into the air. The path of the ball is modeled by the equation h = t2 + 10t where h represents the height (in feet) of the ball after t seconds. The graph of this equation is shown to the right. Use this graph to answer the questions.
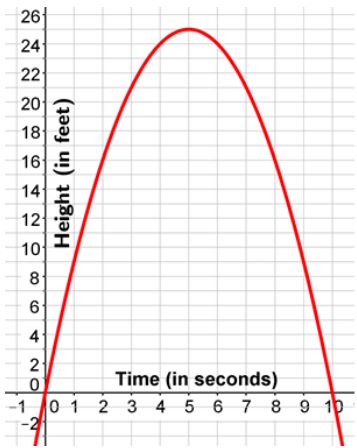
1. What is the maximum height of the ball? How many seconds after being thrown does this occur?
After ___blank seconds, the maximum height of the ball is ___blank feet in the air.
Answer: 5, 25
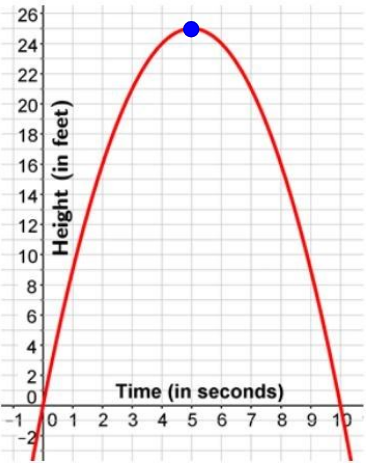
2. How long does it take for the ball to hit the ground?
After ___blank seconds, the ball will reach the ground. This occurs when h = 0.
Answer: 10
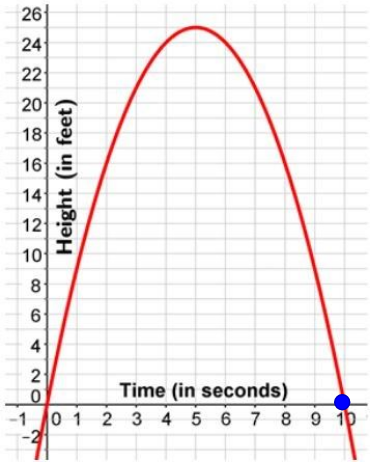
3. What will be the height of the ball after 3 seconds?
After 3 seconds, the height of the ball will be ___blank feet.
Answer: 21
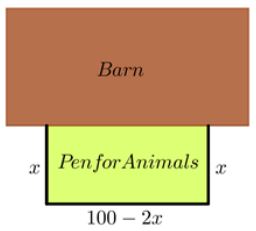
Practice Problem #3
A farmer has 100 feet of fencing to build a rectangular pen, using his barn as one side of the enclosure. What dimensions will maximize the area of the pen? What is the maximum area that can be enclosed?
If x-represents the width of the pen, then 100 − 2x represents the length.
The formula for the area is A = lw where l is the length and w is the width.
l = 100 − 2x
w = x
Using this information, you can substitute into the formula, A = lw.
You will have:
A = lw
A = (100 − 2x)(x)
Simplify using the distributive property.
A = lw
A = (100 − 2x)(x)
A = ___blankx − ___blankx2
Answer: 100, 2
The function A = 100x − 2x2 will give you the maximum area for this pen. Rewrite this equation in standard form to A = −2x2 + 100x.
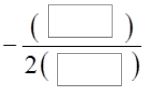
To find the maximum value, find the y-value of the vertex. Substitute 100 for a and −2 for b into the formula for finding the maximum value x = 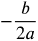 .
.
Simplify.
x = 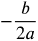 =
= 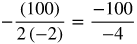 = ____
= ____
Answer: 25
This will give you x − 25, which is the width. Substitute to find the length of the fence.
100 − 2x
100 − 2(25)
100 − ___blank
Answer: 50
100 − 50 = ___blank
Answer: 50
You have w = 25 feet and l = 50 feet. Use this to find the area using the formula A = lw.
A = lw
A = (25)(50)
A = ___blank__
Answer: 1250
The corral maximum area has width 25 feet, length 50 feet, and area 1250 ft2.