3.07 Graphing Quadratic Functions in Vertex Form

Learn

Practice Problems

Practice Problem #1

Identify each of the following.

Vertex: ( ___blank, ___blank )

Axis of Symmetry: x = ___blank

Answer: (4, −3), x = 4

Graph the function y = 3(x − 4)² − 3

Plot each of the following.

Vertex: (4, −3)

Axis of Symmetry: x = 4

What does the graph look like?

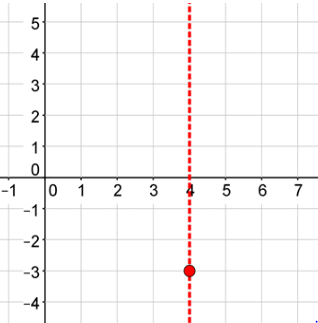
A coordinate plane with a dashed vertical line graphed at x = 4 and a point at (4,negative 3).

Choose a point on the left side of the axis of symmetry and evaluate.

y = 3(x −4)² − 3

y = 3(___blank − 4)² − 3

Answer: 3

Evaluate and simplify

y = 3(−1)² − 3

y = 3(1)− 3

y = 3 − 3

y = 0

Graph the point (3, 0).

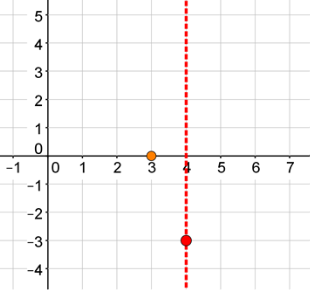
A coordinate plane with a dashed vertical line graphed at x = 4 and points at (4, negative 3) and (3,0).

Choose a point on the other side of the Axis of Symmetry with the same y-coordinate. Plot this point.

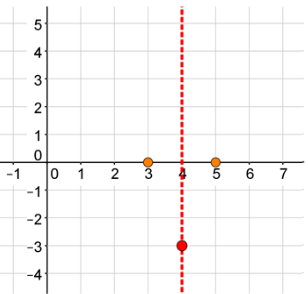
A coordinate plane with a dashed vertical line graphed at x = 4 and points at (4, negative 3), (3,0), and (5,0).

Draw your curve.

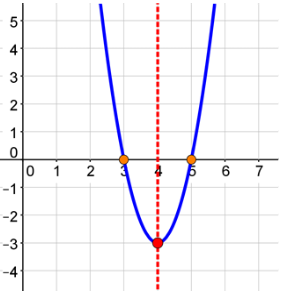
A coordinate plane with a parabola opening up with a dashed vertical line graphed at x = 4 and points at (4, negative 3), (3,0), and (5,0) with the point (4, negative 3) being the vertex.

Practice Problem #2

Find a value for this piece of a parabola.

OK, we can find the vertex from the graph. Using that, we can work backwards by plugging the value of the vertex into the vertex form to solve for a.

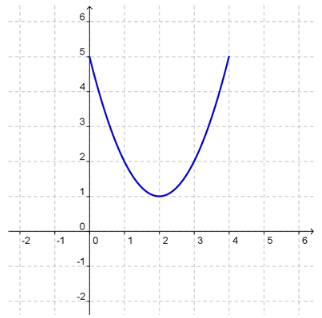
A parabola opening up with a vertex at (2,1) and points at (1,2) ,(3,1), (0,5), and (4,5).

What is the vertex? (___blank, ___blank)

Answer: 2, 1

Now plug these values into the vertex form.

y = a(x − ___blank )² + ___blank

Answer: 2, 1

Great! Let's plug in the ending point values for x and y to solve.

___blank = a( ___blank − 2)² + 1

Answer: 5, 4

Isolate the a term and simplify inside the parenteses.

___blank = a(___blank)²

Answer: 4, 2

Apply the exponent and simplify

4 = ___blanka

Answer: 4

___blank = a

Answer: 1

Practice Problem #3

Find the equation for the highlighted parabola on this image. Find "a". Use the vertex for h and k values and the ending point of the parabola as x and y values. In this parabola, vertex is (___blank, ___blank) and one of the ending points is (___blank, 11)

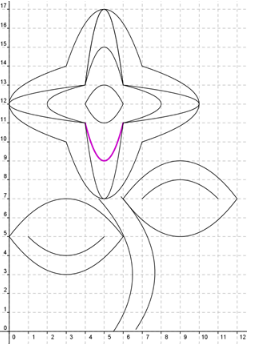
The first quadrant of a coordinate plane with a flower graphed from different curves. A curve is highlighted that is a parabola opening up with a vertex at (5,9) and endpoints at (4,11) and (6,11).

Answer: Vertex (5, 9) and one of the ending points (4, 11)

Plug these values into the vertex form.

___blank = a(___blank − ___blank)² + ___blank

Answer: 11, 4, 5, 9

Isolate the a term and simplify inside the parentheses.

___blank = a(___blank)²

Answer: 2, −1

Solve for a.

a = ___blank

Answer: 2

Great! Now to find the equation, we simply substitute in the values of a, h, and k into the vertex form.

y = ___blank(x − ___blank)² + ___blank

Answer: 2, 5, 9

Practice Problem #4

Find the equation for the highlighted parabola on this image.

Find "a". Use the vertex for h and k values and the ending point of the parabola as x and y values.

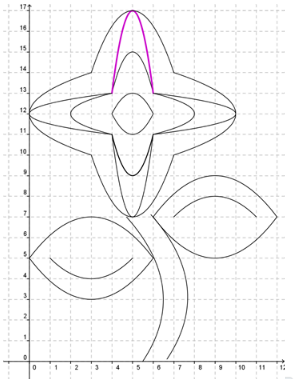
The first quadrant of a coordinate plane with a flower graphed from different curves. A curve is highlighted that is a parabola opening down with a vertex at (5,17) and endpoints at (4,13) and (6,13).

In this parabola, vertex is (___blank, ___blank) and one of the ending points is (4, ___blank)

Answer: Vertex is (5, 17) and ending point is (4, 13)

Plug these values into the vertex form.

___blank = a( ___blank − ___blank )² + ___blank

Answer: 13, 4, 5, 17

Isolate the a term and simplify inside the parentheses.

___blank = a( ___blank )²

Answer: −4, −1

Solve for a.

a = ___blank

Answer: −4

Great! Now to find the equation, we simply substitute in the values of a, h, and k into the vertex form.

y = ___blank (x − ___blank )² + ___blank

Answer: −4, 5, 17

Practice Problem #5

Find the equation for the highlighted parabola on this image.

Find "a". Use the vertex for h and k values and the ending point of the parabola as x and y values.

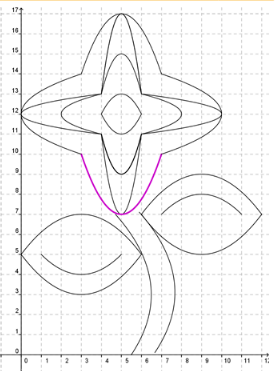
The first quadrant of a coordinate plane with a flower graphed from different curves. A curve is highlighted that is a parabola opening up with a vertex at (5,7) and endpoints at (3,10) and (7,10).