Learn

Vertex Form

Vertex Form of a Quadratic Function

You have previously studied the standard from for a quadratic function. In this lesson, you will examine the vertex form and how it can be used to graph a quadratic function.

Vertex Form: y = a(x − h)2 + k

In the function above, a is the leading coefficient and (h, k) represents the vertex of the parabola.

To find the vertex of the parabola, you will use the values for h and k from the equation.

For example, if you have y = (x − 3)2 + 5, the vertex will be the coordinate point (3, 5).

You will notice that you have a minus inside the parentheses, but the x value of the vertex is positive.
Hint! When you find the x-value of the vertex, tell yourself to take the opposite of the value inside the parentheses.

(h, k) is the vertex. The a in this equations is not the same a in the standard form. It determines how wide or narrow the graph is. You saw in the explore how the a affects the graph.

  • If a > 1 or a < −1, then the graph becomes skinnier. This is called a vertical stretch.
  • If −1 < a < 0 or 0 < a <1, then the graph becomes wider. This is called a vertical shrink or compression.
  • If a < 0 or if a is negative, then the graph is flipped down. This is called a reflection over the x-axis.

Example #1

Determine the vertex, axis of symmetry, and direction of opening of the function
y = −4(x + 1)2 + 7

The vertex is (___blank , ___blank ).

Answer: (−1, 7)

The axis of symmetry is x = ___blank. Reminder: the axis of symmetry is the x-coordinate of the vertex.

Answer: x = −1

The parabola opens ___blank (up or down).

Answer: Down

To determine if the parabola opens up or down, look at the "a" term of the equation. If it's positive, the parabola will open up. If it's negative, the parabola will open down.

Example #2

Determine the vertex, axis of symmetry, and direction of opening of the function y = 5(x − 13)2 = − 4.

The vertex is ( ___blank, ___blank).

Answer: (13, −4)

The axis of symmetry is x = ___blank.

Answer: x = 13

The parabola opens ___blank. (up or down?)

Answer: Up

Graphing

Graphing the Vertex Form

To graph a parabola in vertex form, follow these steps.

  1. Determine the vertex.
  2. Determine the axis of symmetry.
  3. Plot these features on the coordinate plane.
  4. Determine the direction of opening.
  5. Pick an x-value on one side of the parabola and evaluate the function. You will have the same point on the other side of the plane equidistant from the axis of symmetry.
  6. Draw your curve.

Example #3

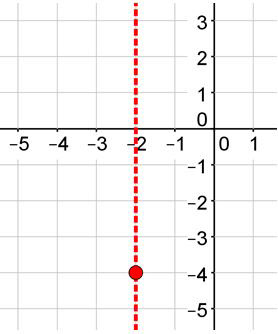
Grab the parabola y = (x + 2)2 − 4.

Step 1: Determine the vertex of the parabola.
The vertex is ( −2 , −4 )

Step 2: Determine the axis of symmetry.

The axis of symmetry is x = ___blank.

Answer: x = −2

Step 3: Plot these features on the coordinate plane.

A coordinate plane with a dashed vertical line at x equals negative 2 with a point at (negative 2, negative 4).

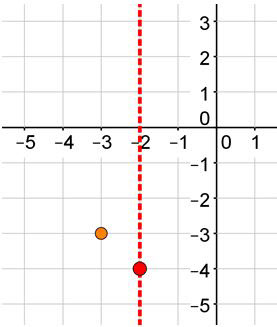
Step 4: Choose an x-value on the left sides and evaluate the function. Suppose you choose x = −3.

Substitute x = −3 to see the corresponding y-value.

y = (x + 2)2 − 4

y = (−3 + 2)2 − 4

y = (−1)2 − 4

y = 1 − 4

y = − 3

Evaluate to find the next point. Plot (−3, −3).

A coordinate plane with a dashed vertical line at x equals negative 2 with points at (negative 2, negative 4) and at (negative 3, negative 3).

Step 5: Plot a point on the other side with the same y-value equidistant from the axis of symmetry.

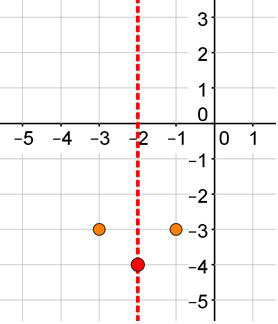
A coordinate plane with a dashed vertical line at x equals negative 2 with points at (negative 2, negative 4), (negative 3, negative 3), and (negative 1, negative 3).

What will be the new point? ( ___blank , ___blank)

Answer: (−1, −3)

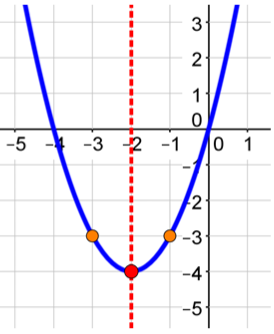
Step 6: Draw your curve.

A coordinate plane with parabola graphed opening up with a dashed vertical line at x equals negative 2 with points at (negative 2, negative 4), (negative 3, negative 3), and (negative 1, negative 3) with (negative 2, negative 4) being the vertex.

Example #4

Graph the function f(x) = −2(x − 3)2 + 4

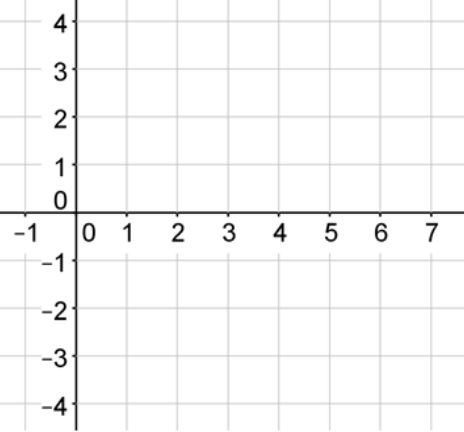
A blank coordinate plane displayed from negative 8 to 9 on the x axis and negative 2 to 19 on the y axis.

Vertex: (3, 4)

Axis of Symmetry: x = ___blank

Answer: x = 3

Plot this on the coordinate plane.

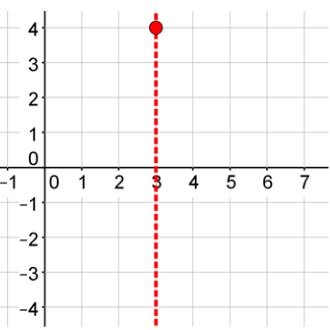
A coordinate plane with a dashed vertical line at x equals 3 with a point at (3, 4).

Pick a point on the left side of the parabola and evaluate the function. Use x = 2.

Evaluate x = 2.

y = −2(x − 3)2 + 4

y = −2(2 − 3)2 + 4

y = −2(−1)2 + 4

y = −2(1) + 4

y = −2 + 4

y = 2

Your next point is (2, 2). Plot this point.

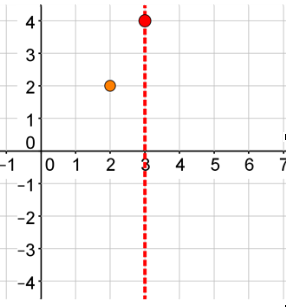
A coordinate plane with a dashed vertical line at x equals 3 with points at (3, 4) and at (2, 2).

Choose the point on the right side of the axis of symmetry with the same y-value and plot this point. Another point is (4, 2).

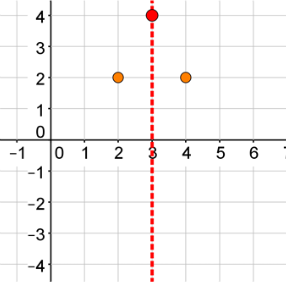
A coordinate plane with a dashed vertical line at x equals 3 with points at (3, 4) , (2, 2), and (4,2).

Draw your curve.

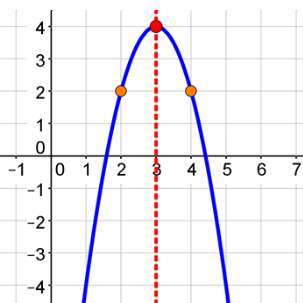
A coordinate plane with a parabola opening down with a dashed vertical line at x equals 3 with points at (3, 4) , (2, 2), and (4,2) with the point (3,4) being the vertex.

Quadratic Equations - Vertex Form

Domain of Quadratic Functions

Find the domain of the following parabola.

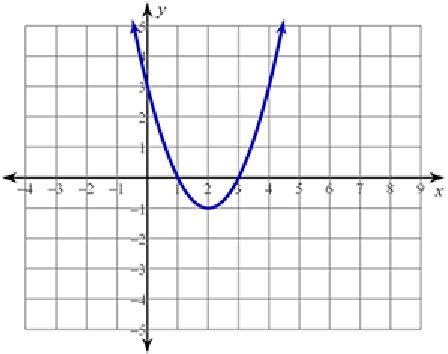
A coordinate plane of a parabola opening up.

Domain is the x-values of a function. When looking at a graph, we will look at what x-values are on the graph. If a graph goes left and right forever, then every x-value is on the graph. If this is true like it is in this graph, the domain is All Real Numbers.

Since all parabolas go left and right forever, the domain will always be All Real Numbers.

Range is the y-values of a function. When looking at a graph, we will look at what y-values are on the graph. If a graph goes up and down forever, then every y value is on the graph. If this is true, then the range is All Real Numbers. This graph, however, does not go up and down forever. Decide next, if the graph goes up forever or down forever. If the graph goes up forever, your range will be y ≥ k. The k of the vertex (h, k) will always be the lowest or highest point on the graph. If the graph goes down forever, the range will be y ≤ k.

Since this graph goes up forever, the range is y ≥ − 1.

Find the domain of the following parabola.

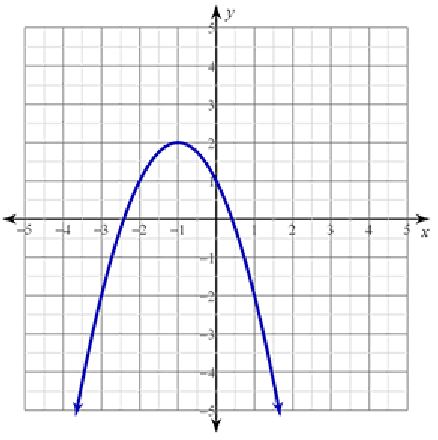
A coordinate plane with a parabola opening down.

Domain: All Real Numbers Remember, the domain is always All Real Numbers for parabolas

Range: y ≤ 2

Since this graph goes down forever, the range is y ≤ k.

Example #5

Change y = 2x2 − 7x + 5 to vertex form. Name the vertex and tell if the vertex is a relative maximum or minimum. Find a in the vertex form and tell if this graph is a stretch or shrink.

y=2x2−7x+5

First, we need to factor out the two in front of x2. y _____ (Fill in the blank) = 2(x2 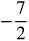negative seven halvesx _____ (Fill in the blank)) +5 We must also divide 7 by 2.

Now. we take half of negative seven over two and square it to fill in the blank on the right.

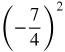Half of minus seven over two=minus seven over fourand minus seven over four squared=49 over 16

Now we have y + 2 (49 over 16) equals 2 times 2 squared minus (7 over 2) x equals (49 over 16)] plus 5

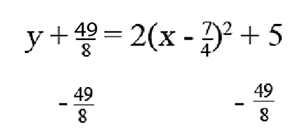
y plus 48 over 8 equals 2 times open parenthesis x minus seven fourths close parenthesis squared plus 5. Then minus 49 over 8 on both sides.

y equals 2 open paren x minus 7 over 40 close paren squared minus open paren 9 over 8 close paren

The vertex is seven over four comma nine over eight

Because a = 2, we know this is a relative minimum and we know that this is a horizontal shrink because | a | > 1.

This was rather complicated, right? Would you like an easy way to check it? Open Geogebra and graph both equations on the same grid. If they are identical then it is correct.

Geogebra

Example #6

Compare the graph of y = 2x2 − 2x + 6 to a parabola with a vertex of (3,1) and an a value of negative one third

We have this graphed to the right. We see that it has a relative minimum and there are no x intercepts. The y intercept is 6.

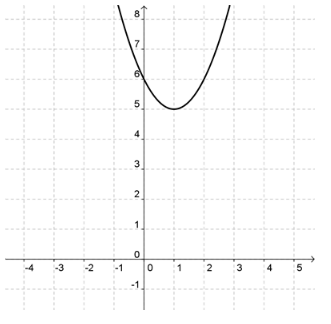
A coordinate plane with a parabola opening up above the x-axis with a vertex at (1,5) and y-intercept at (0,6) and another point at (2,6).

The first function has a vertex of (1,5) which means the graph translated right 1 and up 5. Since a > 0, the graph opens up with a minimum point. Since a > 1, there is a vertical stretch. The second function translates right 3, up 1. Since the a < 0, the graph opens down with a maximum point. Since − 1 < a < 0, there is a vertical shrink or compression.

Example #7

Watch Write the Equation of a Quadratic Function in Vertex Form Given Its Graph.

Open Write the Equation of a Quadratic Function in Vertex Form Given Its Graph in a new tab

Note: The presentation may take a moment to load.

Example #8

Watch Change the Equation of a Quadratic Function from Standard Form to Vertex Form to Identify Different Properties of Its Graph; Graph a Quadratic Function.

Open Change the Equation of a Quadratic Function from Standard Form to Vertex Form to Identify Different Properties of Its Graph; Graph a Quadratic Function in a new tab

Note: The presentation may take a moment to load.