Learn

Practice Problems

Practice Problem #1

Graph y = 3x2− 5x− 2

Step 1) Find the axis of symmetry.

x equals negative b over 2 a.

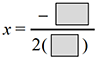
x equals the fraction with numerator negative blank and denominator 2 times open paren blank close paren

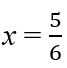
x equals 5 over 6

Step 2) Find the vertex. We know from the first step that 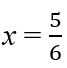x equals 5 over 6

Plug 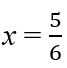x equals 5 over 6 into the equation y = 3x2− 5x− 2 to solve for y.

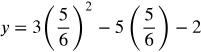
y equals 3(5 over 6)squared minus 5 (5 over 6) minus 2

Evaluate the exponents first.

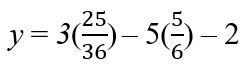
y equals 3(25 over 36) minus 5(5 over 6) minus 2

Evaluate the multiplication next.

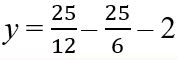
y equals 25 over 12 minus 25 over 6 minus 2

Add by getting a common denominator.

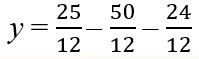
y equals 25 over 12 minus 50 over 12 minus 24 over 12

Subtract.

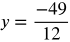
y equals negative 49 over 12

The vertex is 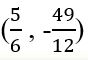open paren five sixths comma negative 49 over 12 close paren.

Step 3) Find the x-intercepts. Set y equal to 0 and solve.

0 = 3x2 − 5x − 2

To solve, factor the equation. Find the factors of a times c that add to equal b.

The factors of −6 that add to equal −5 are−6 and 1.

Remember to divide by a and reduce.

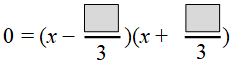
0 equals (x minus blank over 3)(x + blank over 3)

Answer: 6 ,1

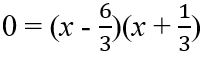
0 equals (x− 6/3)(x + 1/3)

0 equals (x minus 2)(x + 1 over 3)

x−2 = 0 or x + 1 over 3= 0

x = 2 or x = negative one third

Axis of Symmetry: 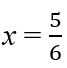x = 5/6

Vertex: 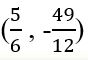open paren five sixths comma negative 49 over 12 close paren

x-intercepts: (negative one third, 0) and (2, 0)

Step 4) Find the y-intercept. The y-intercept is the c value.

c =

The y-intercept is (0, −2).

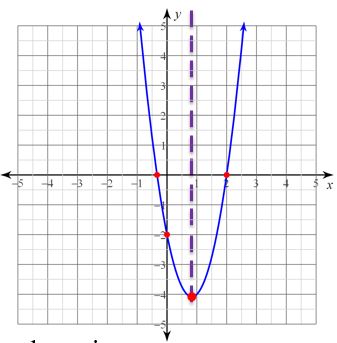
We will now graph everything that we have found.

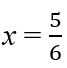
  • Axis of symmetry: x equals 5 over 6
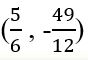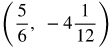
  • The vertex is: open paren five sixths comma negative 49 over 12 close paren or open paren five sixths comma negative 4 and 1 over 12 close paren
  • x-intercepts: (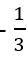negative one third, 0) and (2, 0)
  • y-intercept: (0, −2)

Now, draw a quadratic curve connecting the points.

A coordinate plane with a graph of a parabola opening up with points plotted at (negative one third, 0), (2, 0), (0, negative 2), and (5 sixths, negative 49 over 12) and a dashed line at x = 5 sixths.

Practice Problem #2

Determine the vertex of the function f(x) =−4x2− 16x + 2.

Why did the example use f(x) instead of y?

Hint: Always remember that f(x) can always be used in place of y. They both have the same meaning.

Using the formula x equals minus b over two a, find the x-coordinate of the vertex.

Substitute for b =−16 and a =−4. The negative on the outside must remain outside the parentheses.

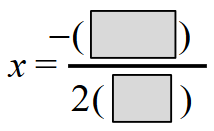
x equals minus blank over 2 times blank

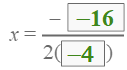
x equals minus minus 16 over 2 minus 4

Simplify the numerator and denominator.

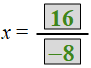
x equals 16 minus 8

x = ___blank

You just found the x-coordinate to be x = −2. Substitute this value into the original equation to find the y-coordinate.

f(x) = −4(−2)2− 16 (−2) + 2

Simplify using the order of operations.

y = −4( ___blank ) + ___blank + 2

Simplify using the order of operations.

y = ___blank + 32 + 2

Simplify using the order of operations.

y = ___blank

You found that x =−2 and y = 18. What is the vertex of your parabola?

( ___blank, ___blank )

  1. Find the vertex of y = 3x2 + 12x + 2
    1. (2, 38)
    2. (−2, −10)
    3. (−2, −34)
    4. (2, 36)

    Answer: b. (−2, −10)

  2. Find the axis of symmetry for y = 4x2 + 16x − 2.
    1. x = 8
    2. x = −8
    3. x = −2
    4. x = 2

    Answer: c. x = −2

  3. Find the y-intercept of y = x2 − 5x − 14
    1. (0, 14)
    2. (−7, 0) and (2, 0)
    3. (7, 0) and (2, 0)
    4. (0, −14)

    Answer: d. (0, −14)

  4. Find the x-intercept(s) of y = x2 − 5x − 14
    1. (0, 14)
    2. (0, −14)
    3. (−7, 0) and (2, 0)
    4. (7, 0) and (−2, 0)

    Answer: d. (7, 0) and (−2, 0)

  5. Find the y-intercept of y = 3x2 − 10x − 24
    1. (0, −8)
    2. (0, −24)

    Answer: b. (0, −24)