Learn

Properties

What is a Quadratic Function?

A Quadratic Function is an equation where each x-value corresponds to only one y-value. The graph will appear as a "U" shaped graph. The graph is called a parabola. The parabolas below are examples of quadratic functions.

three “U” shaped graphs

Hint: Remember that function notation is f(x) and the graph of an equation us y =. These two are interchangable and you will see both during this unit.

Key Properties of Graphs

The graph of a quadratic function may appear simple, but there are many different properties to the graph. The following is a list of the properties which you will study during this lesson:

  • Positive or Negative Parabola
  • Vertex of the Parabola
  • Axis of Symmetry
  • Maximum and Minimum Values
  • Intervals of Increasing and Decreasing
  • x-intercept(s)
  • y-intercept

Positive or Negative Parabola

The standard form of a parabola, or quadratic equation, is:

y = ax2 + bx + c

If the value of a is greater than zero, the parabola will open up and will be a positive parabola.

positive parabola opening up

If the value of a is less than zero, the parabola will open down and will be a negative parabola.

Negative parabola opening down

The Vertex of a Quadratic

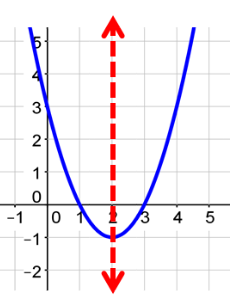
The graph below is a positive quadratic function.

The next property to identify is the vertex of the function. The vertex can be thought of as the turning point of the graph.

A coordinate plane with a graph of a parabola opening up with a vertex at (2, negative 1).

The Axis of Symmetry of a Quadratic

The graph below is a positive quadratic function.

The axis of symmetry is the vertical line that passes through the vertex. If you were to draw this graph on a piece of paper and fold along the axis of symmetry, each side of the graph would align.

A coordinate plane with a graph of a parabola opening up with a vertex at (2, negative 1) and a dashed vertical line at x = 2.

Maximum and Minimum Values

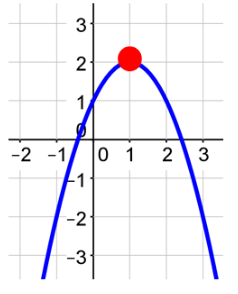
The graph below is a positive quadratic function.

The minimum value of a quadratic is the lowest point on the graph. The minimum value is the same coordinate as the vertex of the function. You will have a minimum value if your graph opens up, or in other words, is positive.

A coordinate plane with a graph of a parabola opening up with a vertex at (2, negative 1).

The graph below is a negative quadratic function.

The maximum value of a quadratic is the highest point on the graph. The maximum value is the same coordinate as the vertex of the function. You will have a maximum value if your graph opens down, or in other words, is negative.

A coordinate plane with a graph of a parabola opening down with a vertex at (1, 2).

Increasing Interval of a Quadratic

The graph below is a positive quadratic function.

The interval where the graph is increasing occurs where the graph appears to be climbing uphill.

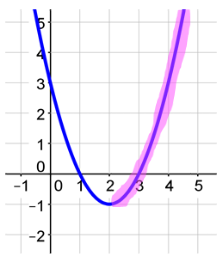
A coordinate plane with a graph of a parabola opening up with a vertex at (2, negative 1). The right side of the parabola starting at the vertex is highlighted.

Decreasing Interval of a Quadratic

The graph below is a positive quadratic function.

The interval where the graph is decreasing occurs where the graph appears to be falling downhill.

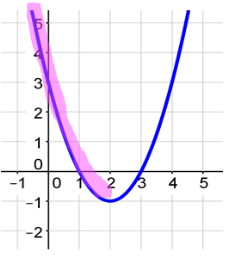
A coordinate plane with a graph of a parabola opening up with a vertex at (2, negative 1). The left side of the parabola ending at the vertex is highlighted.

The x-intercepts

The graph below is a positive quadratic function.

The x-intercepts of the graph are the intersections of the graph and the x-axis. The x-intercepts play an important role in the solution to the equation of the quadratic. Quadratic functions will have zero, one, or two x-intercepts.

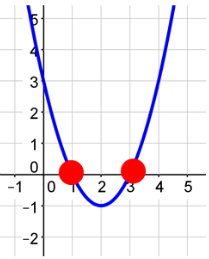
A coordinate plane with a graph of a parabola opening up with a vertex at (2, negative 1) that passes through the x-axis at 1 and 3. The graph has red points at (1,0) and (3,0).

The y-Intercepts

The graph below is a positive quadratic function.

The y-intercept of the graph is the intersection of the graph and the y-axis. The y-intercept will also be the constant term of the function. Quadratic functions will have one y-intercept.

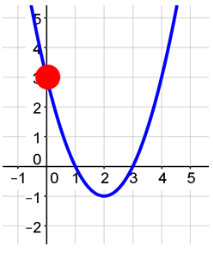
A coordinate plane with a graph of a parabola opening up with a vertex at (2, negative 1) that passes through the y-axis at 3. The parabola has a red point at (0,3).

Example #1

The graph below is f(x) = x2 + 8x + 12. Identify the key features of the graph.

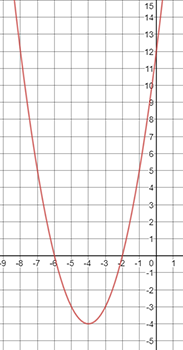
A coordinate plane with a graph of a parabola opening up with a vertex at (negative 4, negative 4) that passes through the x-axis at negative 2 and negative 6 and passes through the y-axis at 12.

Is this a positive or negative parabola?

Answer: This is a positive parabola because it is opening up. You also know this is a positive parabola because the value of a is 1 which is greater than 0.

What is the vertex of the function?

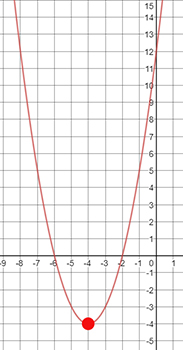
A coordinate plane with a graph of a parabola opening up with a vertex at (negative 4, negative 4) that passes through the x-axis at negative 2 and negative 6 and passes through the y-axis at 12. There is a red point at (2, negative 1).

( ___blank , ___blank )

Answer: (−4, −4)

What is the equation for the axis of symmetry?

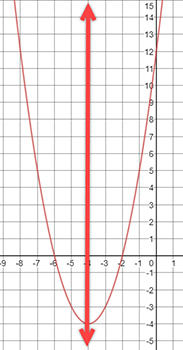
A coordinate plane with a graph of a parabola opening up with a vertex at (negative 4, negative 4) that passes through the x-axis at negative 2 and negative 6 and passes through the y-axis at 12. There is a red vertical line at x = negative 4.

x = ___blank

Answer: x = −4

What is the maximum or minimum point for the graph? Because this graph opens up, you will only have a minimum value. The minimum value occurs at the vertex. The minimum value is the same as the vertex, (−4, −4).

A coordinate plane with a graph of a parabola opening up with a vertex at (negative 4, negative 4) that passes through the x-axis at negative 2 and negative 6 and passes through the y-axis at 12. There is a red point at (2, negative 1).

Where is the graph increasing?

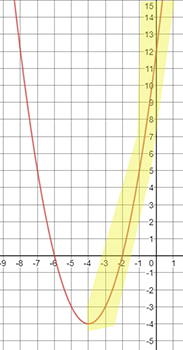
A coordinate plane with a graph of a parabola opening up with a vertex at (negative 4, negative 4) that passes through the x-axis at negative 2 and negative 6 and passes through the y-axis at 12. The right side of the parabola starting at the vertex is highlighted.

The graph begins increasing at an x-value of −4 and continues to the right indefinitely. The interval will be (−4, ∞). Hint! Always remember that graphs continue indefinitely to the left and to the right. When indicating "indefinitely" in math terms, you will use the infinity symbol (∞). You can have one of two possibilities for your intervals of increasing and decreasing: (x, ∞) or (−∞, x). x represents the x-coordinate of the vertex.

Where is the graph decreasing?

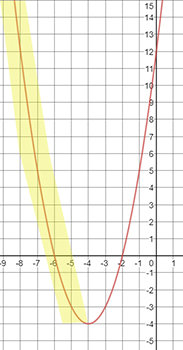
A coordinate plane with a graph of a parabola opening up with a vertex at (negative 4, negative 4) that passes through the x-axis at negative 2 and negative 6 and passes through the y-axis at 12. The left side of the parabola ending at the vertex is highlighted.

The graph begins decreasing at an indefinite x-value and continues to an x-value of −4. The interval will be (-∞, −4).

What are the x-intercepts of the graph?

( __ , 0) ( __ , 0)

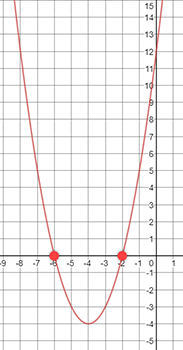
A coordinate plane with a graph of a parabola opening up with a vertex at (negative 4, negative 4) that passes through the x-axis at negative 2 and negative 6 and passes through the y-axis at 12. There are red points at (negative 6, 0) and (negative 2, 0).

Answer:

(−6, 0)

(−2, 0)

What is the y-intercept of the graph? (0, ___blank )

A coordinate plane with a graph of a parabola opening up with a vertex at (negative 4, negative 4) that passes through the x-axis at negative 2 and negative 6 and passes through the y-axis at 12. There is a red point at (0, 12).

Answer: (0, 12)

The graph below is f(x) = x2 + 8x + 12.

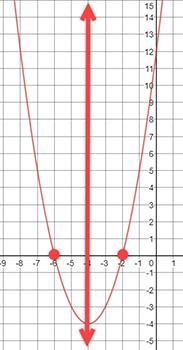
A coordinate plane with a graph of a parabola opening up with a vertex at (negative 4, negative 4) that passes through the x-axis at negative 2 and negative 6 and passes through the y-axis at 12. There are red points at (negative 6, 0) and (negative 2, 0). There is a red vertical line at x = negative 4.

Summary of Key Features:

  • Positive Parabola
  • Vertex: (−4, −4)
  • Axis of Symmetry: x = −4
  • Increasing: (−4, ∞ )
  • Decreasing: (−∞ , −4)
  • Minimum Value: (−4, −4)
  • x-intercepts: (−6, 0) and (−2, 0)
  • y-intercept: (0, 12)

Example #2

The function is graphed below f(x) = −2x2 − 4x −4. Identify the key features of the graph. Is this a positive or negative parabola?

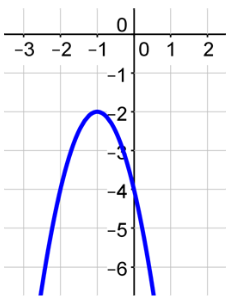
A coordinate plane with a graph of a parabola with a vertex at (negative 1, negative 2) below the x-axis opening down, so there are not any x-intercepts. The graph passes through the y-axis at (0,-4).

Answer: This is a negative parabola because it is opening down. You also know this is a negative parabola because the value of a is −2 which is less than 0.

What is the vertex of the function?

(___blank, ___blank)

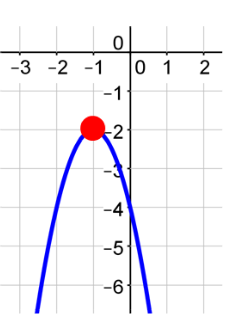
A coordinate plane with a graph of a parabola with a vertex at (negative 1, negative 2) below the x-axis opening down, so there are not any x-intercepts. The graph passes through the y-axis at (0,-4). There is a red point at (negative 1, negative 2).

Answer: (−1, −2)

What is the equation for the Axis of Symmetry?

x = ___blank

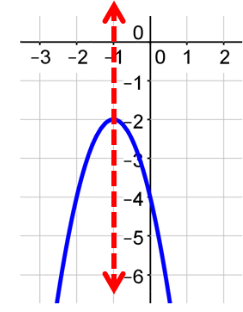
A coordinate plane with a graph of a parabola with a vertex at (negative 1, negative 2) below the x-axis opening down, so there are not any x-intercepts. The graph passes through the y-axis at (0,-4). There is a vertical dashed line at x = negative 1.

Answer: x = −1

What is the maximum or minimum point for the graph? Because this graph opens down, you will only have a maximum value. The maximum value occurs at the vertex. The maximum value is (−1, −2).

A coordinate plane with a graph of a parabola with a vertex at (negative 1, negative 2) below the x-axis opening down, so there are not any x-intercepts. The graph passes through the y-axis at (0,-4). There is a red point at (negative 1, negative 2).

Where is the graph increasing?

The graph begins increasing at an indefinite x-value and continues to an x-value of −1. The interval will be (-∞ , −1).

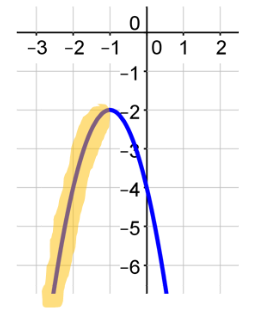
A coordinate plane with a graph of a parabola with a vertex at (negative 1, negative 2) below the x-axis opening down, so there are not any x-intercepts. The graph passes through the y-axis at (0,-4). The left side of the graph is highlighted ending at the vertex.

Where is the graph decreasing? The graph begins decreasing at an x-value of −1 and continues to the right indefinitely. The interval will be (−1, ∞ ).

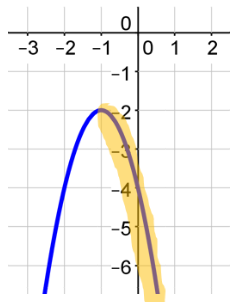
A coordinate plane with a graph of a parabola with a vertex at (negative 1, negative 2) below the x-axis opening down, so there are not any x-intercepts. The graph passes through the y-axis at (0,-4). The right side of the graph is highlighted starting at the vertex.

What are the x-intercepts of the graph? There are no x-intercepts to this graph because the graph does not intersect the x-axis.

What is the y-intercept of the graph?

(0, ___blank )

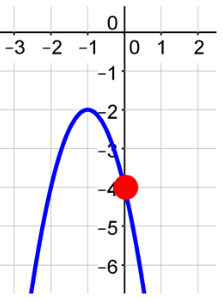
A coordinate plane with a graph of a parabola with a vertex at (negative 1, negative 2) below the x-axis opening down, so there are not any x-intercepts. The graph passes through the y-axis at (0,-4). There is a red point at (0, negative 4).

Answer: (0, −4)

The graph below is the graph of f(x) = −2x2 − 4x − 4.

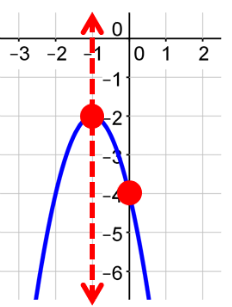
A coordinate plane with a graph of a parabola with a vertex at (negative 1, negative 2) below the x-axis opening down, so there are not any x-intercepts. The graph passes through the y-axis at (0,-4). There is a red point at (0, negative 4) and a vertical dashed line at x = negative 1.

Summary of the Key Features

  • Negative Parabola
  • Vertex: (−1, −2)
  • Axis of Symmetry: x = −1
  • Increasing: (−∞, −1)
  • Decreasing: (−1, ∞ )
  • Maximum Value: (−1, −2)
  • x-intercepts: None
  • y-intercept: (0, −4)

Axis of Symmetry

Example #3 Axis of Symmetry

There is a formula for finding the axis of symmetry of a quadratic equation:

y = ax2 + bx + c, x equals negative b over two a

Example: y = x2 + 4x + 1

Steps:

List a, b: a = ___blank b = ___blank

Answer: a = 1, b = 4

Plug into the formula: x equals negative b over two a : x equals negative four over two times one

Simplify: x = ___blank

Answer: x = −2

The Vertex

Did you notice anything from the previous problems?

When the vertex is (−1, −4) the axis of symmetry is x = −1.

When the vertex is (3, −4) the axis of symmetry is x = 3.

When the verted os (−4, −4) the axis of symmetry is x = −4.

So if we have the axis of symmetry, we have one value of the vertex. All we need to do is evaluate the equation and we will have the other value.

Example #4 Vertex

Steps: Find the axis of symmetry

We found this in the previous problem: x = −2

Plug in the x value: y = ( ___blank )2 + 4( ___blank ) + 1

Answer: −2, −2

Simplify: y = ___blank − ___blank + 1 = ___blank

Answer: 4, 8, −3

The vertex is ( ___blank, ___blank )

Answer: −2, −3

The x and y Intercepts

It is easy to find or at least estimate the x and y intercepts when graphing. How does this connect algebraically?

Look at the graph of y = x2 + 5x + 6

A coordinate plane with a graph of the quadratic function y = x squared plus 5x plus 6. The parabola has a vertex below the x-axis opening up passing through negative 2 and negative 3 on the x-axis and 6 on the y-axis.

Name the y intercept: y = ___blank

Answer: 6

Name the x intercepts: x = ___blank and x = ___blank

Answer: −3, −2

Notice the y intercept is c in the equation. If we move the −3 and the −2 to the left hand side we would have x + 3 = 0 and x + 2 = 0.

These are factors of:

y = x2 + 5x + 6

(x + 3)(x + 2) = 0

Example #5 the x and y Intercepts

Using the equation y = x2 − 4x − 5, find find the y-intercept, x-intercept(s), axis of symmetry, and then graph.

In this equation, a = ___blank, b = ___blank, c = ___blank

Answer: 1, −4, −5

This means the y intercept is y = ___blank

Answer: −5

The x intercepts are found by factoring:

(x − 5)(x + 1) = y and solving x − 5 = 0 and x + 1 = 0 so the x intercepts are x = ___blank and x = ___blank.

Answer: 5, −1

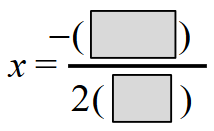
The axis of symmetry: x equals negative b over two a x equals negative blank over two times blank

Answer: −4/1

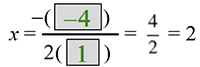
x equals the fraction with numerator negative negative 4 and denominator 2 times 1 equals four halves equals 2

Simplify. The axis of symmetry is x = ___blank.

Answer: 2

Plug in x to get the rest of the vertex:

y = ( ___blank )2 −4( ___blank ) − 5 = ___blank

Answer: 2, 2, −9

Vertex is ( ___blank, ___blank )

Answer: 2, −9

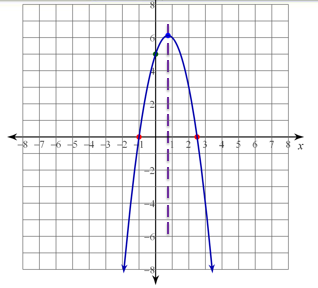
Now let's graph.

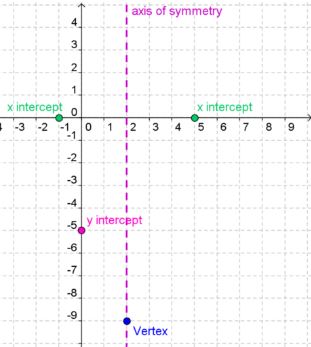
A coordinate plane with points plotted at (negative 1,0) and (5,0) labeled x-intercept for both, a point plotted at (0, negative 5) labeled y-intercept, a point plotted at (2, negative 9) labeled vertex, and a dashed vertical line at x = 2 labeled axis of symmetry.

Because a = 1, so the graph opens up

The y intercept is y = −5.

The x intercepts are x = 5 and x = −1.

What was the axis of symmetry? x = 2

The axis of symmetry is graphed with a dashed vertical line.

Vertex is (2, −9).

Now complete the parabola.

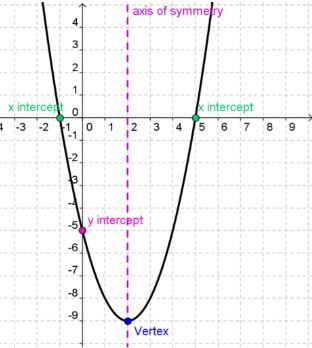
A coordinate plane with a parabola opening up with points plotted at (negative 1,0) and (5,0) labeled x-intercept for both, a point plotted at (0, negative 5) labeled y-intercept, a point plotted at (2, negative 9) labeled vertex, and a dashed vertical line at x = 2 labeled axis of symmetry.

Graphing Quadratic Equations

Example #6

Graph y = −2x2 + 3x + 5

Step 1: Find the axis of symmetry.

x equals negative b over two a

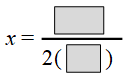
x equals blank over two times blank

x equals negative 3 over negative 4

x equals three fourths

Axis of Symmetry : x = 3/4

Step 2: Find the vertex.

We know from Step 1 that x equals three-fourths

y = −2x2 + 3x + 5

Plug x equals three-fourths into the equation to solve for y.

y = minus two open parent three-fourths close paren squared plus 3 times open paren 3 slash 4 close paren plus 5 Evaluate the exponents first.

y equals negative 2 times open paren nine-sixteenths close paren plus 3 times three-fourths plus 5 Evaluate the multiplication next

y equals minus nine eighths plus nine fourths plus five Add by getting a common denominator

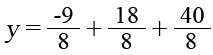
y equals minus nine eighths + eighteen over eight + forty over eight

y equal 49 over 8

Vertex: (three fourths) , (49 over 8)

Step 3: Find the x-intercepts. Set y equal to 0 and solve.

0 = −2x2 + 3x + 5 To solve, factor the equation. Since a is negative, factor out the negative 1.

0 = −1(2x2 − 3x − 5)

Find the factors of a times c that add to equal b.

The factors of −10 that add to equal −3 are −5 and 2.

0 = minus 1 (x − 5 over 2)(x + 2 over 2) Remember, to divide by a and reduce.

0 = minus 1(x minus 5 over 2)(x + 1) Since we are solving, we do not have to move the 2 to the front of the factor.

−1 ≠ 0 or x minus 5 over 2 = 0 or x + 1 = 0

x = x minus 5 over 2 ; x = −1

x-intercepts: ( 5 over 2, 0) and (−1, 0)

Step 4: Find the y-intercept. The y-intercept is the c-value.

c = 5

The y-intercept is (0,5)

Graph y = −2x2 + 3x + 5

We will now graph everything that we have found.

Because a = −2, so the graph opens down

Axis of Symmetry : x = 3 over 4

Vertex: (3 over 4) , (49 over 8)

x-intercepts: ( 5 over 2, 0) and (−1, 0)

The y-intercept is (0,5)

Now, draw a quadratic curve connecting the points.

A coordinate plane a graph of a parabola opening down with points plotted at (negative 1, 0), (2.5, 0), (0,5), and (3 fourths, 49 eighths) and a dashed line at x = 3 fourths.

The axis of symmetry is graphed with a dashed vertical line.