Practice
Practice Problems
Practice Problem #1
Solve the quadratic equation m2 − 5m = 0
The solutions are m = ___(Fill in the blank) and m = ___(Fill in the blank).
The solutions are m = 0 and m = 5.
When you factor out the GCF, you will have:
m(m − 5) = 0
When you solve the quadratic equation, you will have:
- m = 0
- m − 5 = 0
- m = 5
Therefore, your two solutions are m = 5 and m = 0.
Practice Problem #2
Solve the quadratic equation 4x2 + 28x + 49 = 0
The solutions are x = − 
= −
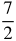
Use the perfect square trinomial method to factor. Find the square root if the first term and last term of the equation. This will give you:
- (2x + 7)(2x + 7) = 0 or (2x + 7)2 = 0
When you solve, you will have only one solution:
- 2x + 7 = 0
- 2x = −7 (Subtracted 7 on both sides)
- x = − 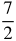(Divided by 2 on both sides to isolate the variable)
The solution is x = −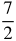
Practice Problem #3
Solve by factoring. x2 − 25 = 0
- x2 − 25 = 0
Factor
(x + 5)(x − 5) = 0
The product of two factors is zero if one or both factors equals zero. Set each factor equal to zero and solve for those numbers.
x + 5 = 0 or x − 5 =0
- x = −5 or x = 5
Practice Problem #4
Solve by factoring. x2 + 4 = 0
- x2 + 4 = 0
Factor
(x + 2i)(x − 2i) = 0
The product of two factors is zero if one or both factors equals zero. Set each factor equal to zero and solve for those numbers.
x + 2i = 0 or x − 2i =0
- x = −2i or x = 2i
Practice Problem #5
Solve by factoring. 2x2 − 12 = 2x
We need to factor this. So, let us start!
Step 1: Set this equal to zero.
2x2−___(Fill in the blank) − 12 = 0
2x2− 2x − 12 = 0
Step 2: Factor.
2x2− 2x − 12 = 0 factors into:
2(x2 − ___(Fill in the blank) − ___(Fill in the blank))
2(x2 − x − 6) = 2(x − __(Fill in the blank)) (x + __(Fill in the blank))
2(x2 − x − 6) = 2(x − 3) (x + 2)
Step 3: The product of two factors is zero if one or both factors equals zero. Set each factor equal to zero and solve for those numbers.
x − 3 = 0
x = ___(Fill in the blank)
x = 3
AND
x + 2 = 0
x = ___(Fill in the blank)
x = −2