Learn

Solving Quadratic Equations by Factoring

What is a quadratic function?

Before we begin reviewing factoring, let us review what a quadratic function is:

An example of a Quadratic Equation:

3x2 + 2x − 1 = 0

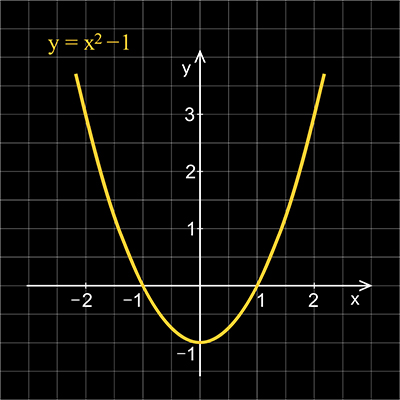
Quadratic Equations make curved graphs, like this one. The graph of a quadratic function is called a parabola.

A coordinate plane with a parabola opening up with a vertex at (0,-1).

Zero Product Property

Given a × 8 = 0, which of the following must be true about a?

  1. a must be 0.
  2. a can be any number.

Answer:

    A. a must be 0.

The zero product property states that for any real numbers a and b, if ab = 0, then a = 0 or b = 0 or both a = 0 and b = 0.

The zero product property is used to solve quadratic equations written in factored form. Use the following steps to solve quadratic equations in factored form:

  1. Set each factor equal to zero
  2. Solve each equation
  3. Check the solutions

Example #1

Watch Solve Quadratic Equations in Factored Form Using the Zero-Product Property.

Open "Solve Quadratic Equations in Factored Form Using the Zero-Product Property" in a new tab

Example #2

Watch Solve Quadratic Equations in Factored Form Using the Zero-Product Property.

Open "Solve Quadratic Equations in Factored Form Using the Zero-Product Property" in a new tab

Solving Quadratic Equations

Occasionally you will have to factor the quadratic to solve the equation. If you recall, you learned how to factor quadratic expressions previously. You will be required to apply several different techniques of factoring in this unit to solve quadratic equations.

Number of Solutions

You might be wondering how many solutions you will have for a quadratic equation. In the Introduction, you learned you will have zero, one, or two solutions. Two solutions is the greatest number of solutions you will have.

How do you know the greatest number of solutions to a problem?

The number of solutions to an equation is the degree of the equation.

  • This equation will have one solution: x − 4 = 8
  • This equation will have two solutions: x2 − 2x + 1 = 0
  • This equation will have three solutions: x3 − 2x2 + 4x + 1 = 0

Solving Quadratic Functions by Factoring

We will start by reviewing how to factor quadratic equations.

The equation x2 − 9 factors into (x + 3)(x − 3).

Do you remember this is a difference of squares?

a2 − b2 = (a + b)(a − b)

In Algebra I, the expression had to be a difference of squares to be able to factor it, because we only worked with real numbers.

Quadratic Equations with Real Roots

The graph of the equation f(x) = x2 − 9 is shown below.

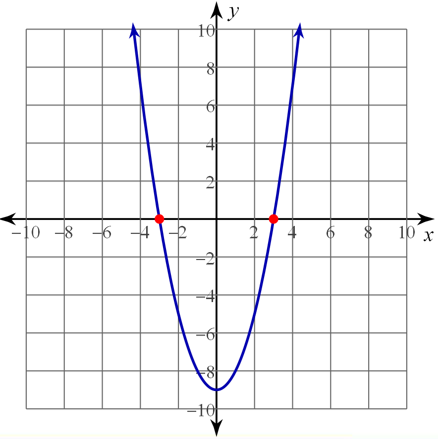
A coordinate plane with a graph of a parabola or u shaped graph opening up with a vertex at (0, negative 9) with two x-intercepts at negative 3 and 3.

If the factors are (x − 3)(x + 3), then x = ±3.

You can see these are the x-intercepts of the graph.

Since x is to the second power, you know we now have 2 solutions.

Quadratic Equations with Complex Roots

Since we have learned about complex numbers, we can now factor sum of squares. If we have an equation: x2 + 9 = 0, we can solve by taking the square root of both sides.

We want to isolate the variable.

First, subtract 9 from both sides.

  • x2 + 9 = 0
  • x2 = −9

Now take the square root of both sides.

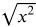  • square root of x squared =
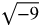
  • x = ±3i

You can look at the graph to see there are not any x-intercepts.

A coordinate plane with a graph of a parabola or u shaped graph opening up with a vertex at (0, 9). The graph is above the x-axis opening up, so there are not any x-intercepts.

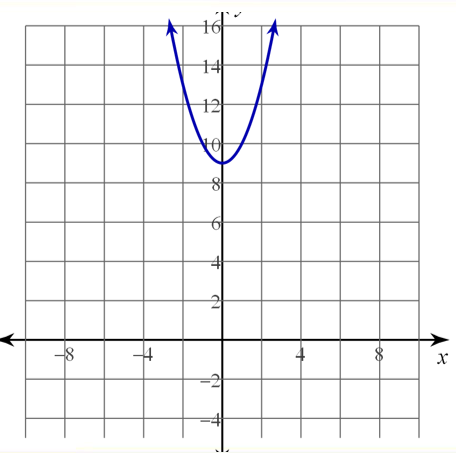
This graph will never cross through the x-axis. Since we do not have any real solutions, there are no x-intercepts on this parabola. Imaginary solutions are not x-intercepts on a graph.

Find the factors of x2 + 9 = 0.

Since we found that x = 3i or x = −3i for this problem, we can get everything to one side to find the factors:

  • x = 3i
  • Subtract 3i from both sides:
  • x − 3i = 0
  • or
  • x = −3i
  • Add 3i to both sides:
  • x + 3i = 0

So, the factors would be (x + 3i)(x − 3i) = 0.

Now, we can factor sum of squares with this formula: a2 + b2 = (a + bi)(a − bi)

Example #3 and #4

Watch Solve Quadratic Equations by Factoring the Sum of Two Squares.

Open "Solve Quadratic Equations by Factoring the Sum of Two Squares" in a new tab

Example #5

Watch Solve a Quadratic Equation Made Up of the Difference of Two Squares by Factoring.

Open Solve a Quadratic Equation Made Up of the Difference of Two Squares by Factoring in a new tab

Reviewing of Factoring Trinomials

Now, we will review factoring trinomials in the form ax2 + bx + c. First, find the factors of a times c that add to equal b. If the factors are p and q, then it will factor into:

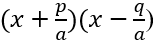
open paren x plus p over a. close paren times open paren x minus q over a. close paren

You will then reduce each fraction by a, then move any remaining denominator to the front of the factor.

Factor Trinomials

To factor trinomials of the form ax2 + bx + c = 0

  1. Find the product of ac.
  2. Find all possible factors of ac.
  3. Determine which factors of ac sum to equal b. These will be p and q.
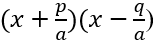
  4. Substitute p and q into the formula open paren x plus p over a. close paren times open paren x minus q over a. close paren
  5. If p and q do not divide evenly by a, make a the coefficient of x in that factor.

Example #6

Watch Solve Quadratic Equations in Standard Form by Factoring.

Open Solve Quadratic Equations in Standard Form by Factoring in a new tab

Example #7

Watch Solve Quadratic Equations in Standard Form by Factoring.

Open "Solve Quadratic Equations in Standard Form by Factoring" in a new tab

Example #8

Watch Solve Quadratic Equations in Standard Form by Factoring.

Open "Solve Quadratic Equations in Standard Form by Factoring" in a new tab

Perfect Squares

Example #9

Watch Solve a Quadratic Equation Made Up of a Perfect Square Trinomial by Factoring.

Open Solve a Quadratic Equation Made Up of a Perfect Square Trinomial by Factoring in a new tab

Grouping

Example #10

Watch Solve Quadratic Equations Using the Factoring by Grouping Method.

Open Solve Quadratic Equations Using the Factoring by Grouping Method in a new tab