Learn

Add and Subtract

Example #1 Matrix Addition

To add 2 matrices together, simply add the elements in corresponding positions. Matrices can only be added if they have the same dimensions.

Watch Add Matrices.

Open Add Matrices in a new tab

Note: The presentation may take a moment to load.

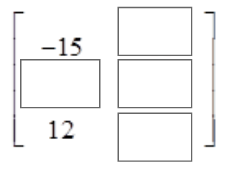
Example #2 Matrix Subtraction

To subtract matrices, simply subtract corresponding elements. Matrices can only be subtracted if they have the same dimensions.

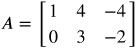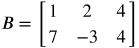
If A equals the 2 by 3 matrix Row-: 1 1 4 negative 4 Row-: 2 0 3 negative 2and B equals the 2 by 3 matrix Row-: 1 1 2 4 Row-: 2 7 negative 3 4

Notice that matrices A and B have the same order 2x3

A minus B equals the 2 by 3 matrix with 1 minus 1, blank minus 2, and negative 4 minus blank in row 1 and Zero minus blank, blank minus negative 3 and negative 2 minus blank in row 2.
A minus B equals the 2 by 3 matrix Row-: 1Column-,- 1 white medium square Column-,- 2 white medium square Column-,- 3 blank Row-: 2Column-,- 1 blank Column-,- 2 blank Column-,- 3 blank

Addition and Subtraction of Matrices

You can add or subtract matrices only if they have the same order.

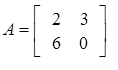
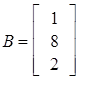
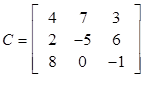
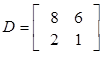
A equals the 2 by 2 matrix Row-: 1 2 3 Row-: 2 6 0B equals the 3 by 1 column matrix 1 8 2C equals the 3 by 3 matrix Row-: 1 4 7 3 Row-: 2 2 negative 5 6 Row-: 3 8 0 negative 1D equals the 2 by 2 matrix Row-: 1 8 6 Row-: 2 2 1

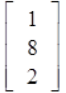
Only A and D are the same order so they can be added or subtracted.

Properties of Matrix Addition

Let A, B, and C be matrices of the same dimensions and let c be a scalar.

  1. A + (B + C) = (A + B) + C Associative Property of Matrix Addition
  2. A + B = B + A Commutative Property of Matrix Addition
  3. c(A + B) = cA + cB Distributive Property

Example #3 Associative Property of Matrix Addition

Watch Use the Associative Property with Matrix Addition.

Open Use the Associative Property with Matrix Addition in a new tab

Note: The presentation may take a moment to load.

Example #4 Commutative Property of Matrix Addition

Watch Understand How the Commutative Property Applies to Matrix Addition.

Open Understand How the Commutative Property Applies to Matrix Addition in a new tab

Note: The presentation may take a moment to load.

Example #5 Distributive Property

Watch Understand the Distributive Property Applies to Matrix Addition.

Open Understand the Distributive Property Applies to Matrix Addition in a new tab

Note: The presentation may take a moment to load.

Additive Identity

The additive identity is the matrix with the same order and with all entries equal to zero.

B = the 3 by 1 column matrix 1 8 2 the additive identity is the 3 by 1 column matrix 0 0 0
If you add these two matrices the 3 by 1 column matrix 1 8 2 + the 3 by 1 column matrix 0 0 0
The result is the original matrix B the 3 by 1 column matrix 1 8 2

Example #6

Watch Use Properties of Matrices to Simplify Matrix Expressions.

Use Properties of Matrices to Simplify Matrix Expressions in a new tab

Note: The presentation may take a moment to load.

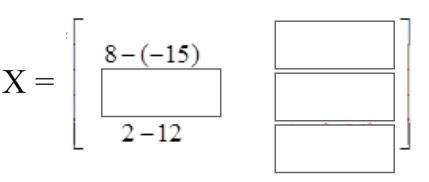
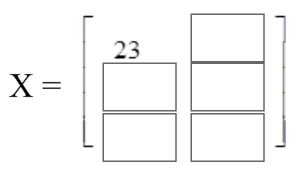
Example #7

Use matrices A and B to solve for X.

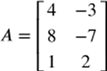
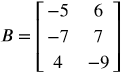
A equals the 3 by 2 matrix Row-: 1 4 negative 3 Row-: 2 8 negative 7 Row-: 3 1 2B equals the 3 by 2 matrix Row-: 1 negative 5 6 Row-: 2 negative 7 7 Row-: 3 4 negative 9

X = 2A − 3B

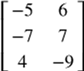X = 2the 3 by 2 matrix Row-: 1 4 negative 3 Row-: 2 8 negative 7 Row-: 3 1 2 − 3the 3 by 2 matrix Row-: 1 negative 5 6 Row-: 2 negative 7 7 Row-: 3 4 negative 9 Do the scalar multiplication first.
X equals a 3 by 2 matrix with 8 and a blank in row 1, blank and blank in row 2, and 2 and blank in row 3. − A 3 by 2 matrix with negative 15 and blank in row 1, blank and blank in row 2, and 12 and blank in row 3.
X equals the 3 by 1 column matrix Row-: 1 8 minus negative 15 blank Row-: 2 blank blank Row-: 3 2 minus 12 blank
X equals a 3 by 2 matrix with 23 and blank in row 1, blank and blank in row 2, blank and blank in row 3.