Learn
Introduction to Matrices
Definition of a Matrix
A matrix is a rectangular arrangement of numbers, symbols, or expressions organized in rows and columns, and enclosed in brackets. The plural of matrix is matrices.
The entries in the matrix are called the elements of the matrix.
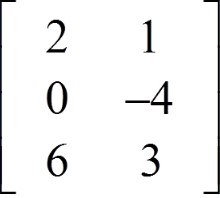
Order of a Matrix
The order of a matrix also called the dimensions, gives the number of rows followed by the number of columns in the matrix.
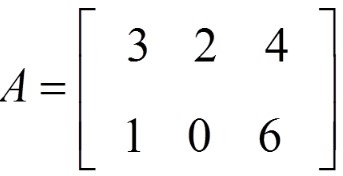
The order of matrix A with 2 rows and 3 columns is written 2 × 3 and is read "2 by 3".
When we need to read out the elements of a matrix, we read it row by row from left to right.
For example: the elements of matrix A are 3, 2, 4Row 1 , 1, 0, 6Row 2
Elements
Each element is defined by its position in the matrix. In matrix C, an element in row i and column j is represented by cij
Examples:
c21=5Second row, first column
c 32 = −3
Try It!
Given the following matrix:
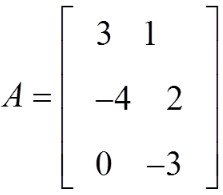
State the order of the matrix
_______ (Fill in the blank) X _______(Fill in the blank)
Element A32 = _______(Fill in the blank)
Element A11 = _______(Fill in the blank)
Element A21 = _______(Fill in the blank)
Special Matrices
Some matrices have special names because of their dimensions or entries.
| Name | Description | Example |
|---|---|---|
| Row Matrix | A matrix with only 1 row | [5 8 12] |
| Column Matrix | A matrix with only 1 column |  |
| Square Matrix | A matrix with the same number of rows and columns | 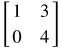 |
| Zero Matrix | A matrix whose entrie are all zero. The zero matrix is also called the null matrix. |  |
Equal Matrices
Two matrices are equal if their orders are the same and their corresponding elements are equal.
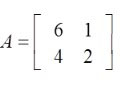
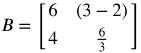
Matrix A = Matrix B
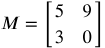
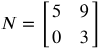
Matrix M ≠ Matrix N
Matrix Equations
Solve the matrix equation for x and y.
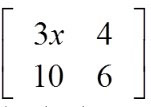 =
=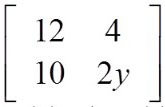
Since the matrices are equal, then each corresponding element must be equal.
Start by setting the elements containing the variables equal to the corresponding element of the other matrix.
3x = (Fill in the blank)_______ 2y (Fill in the blank)_______
x = (Fill in the blank)_______ y = (Fill in the blank)_______
Example #1 Scalar
A real number is often called a scalar. To multiply a matrix by a scalar, each entry in the matrix is multiplied by the scalar.
Watch Multiply Matrices by a Scalar.
Open Multiply Matrices by a Scalar in a new tab
Note: The presentation may take a moment to load.