Try It

Determining Maximum and Minimum Values Guided Practices

Practice Problem #1

Maximize the give objective function within the given constraints:

Objective Function: R(x,y) = 300x + 250y

Constraints: Vertices:
x ≥ 0 (0, 0)
y ≥ 0 (0, 20)
2x + 3y ≤ 60 (15, 10)
4x + 3y ≤ 90 (22.5, 0)

 

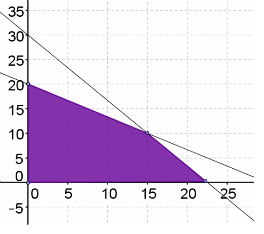
A coordinate plane with four inequalities graphed. The feasible region is in the first quadrant with the vertices (0,20), (15,10), (22.5,0), and (0,0).

Finding Maximum Value

R(0, 0) = 300(0) + 250(0) = 0

R(0, 20) = 300(0) + 250(20) = 5000

R(15, 10) = 300(15) + 250(10) = 7000

R(22.5, 0) = 300(22.5) + 250(0) = 6750

The maximum value is (Fill in the blank)____ and it occurs when x = (Fill in the blank)____ and y = (Fill in the blank)____.

Practice Problem #2

Minimize the given objective function within the given constraints:

Objective Function: R(x,y) = 5x−y

Constraints: Vertices:
y ≥ 10 (20, 50)
x + y ≤ 100 (30, 10)
2x + 5y ≤ 290 (90, 10)
4x + y ≥ 130 (70, 30)

 

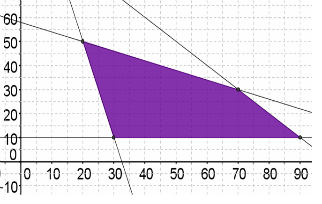
A coordinate plane with four inequalities graphed. The feasible region is in the first quadrant with the vertices (30,10), (90,10), (20,50), and (70,30).

Finding Minimum Value

C(20, 50) = 5(20) − (50) = 50

C(30, 10) = 5(30) − (10) = 140

C(90, 10) = 5(90) − (10) = 440

C(70, 30) = 5(70) − (30) = 320

The minimum value is (Fill in the blank)____ and it occurs when x = (Fill in the blank)____ and y = (Fill in the blank)____

Practice Problem #3

Minimize the objective function: C = 1000x + 1500y

The graph of the feasible region is shown.

HintRemember, find the vertices of the feasible region and plug it into C. The smallest value you can get for C is the minimum value, and the x and y you plugged in are the other answers.

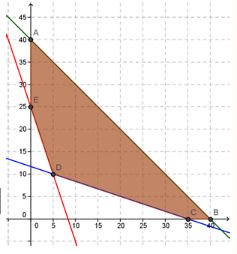
A coordinate plane with a system of inequalities graphed. The feasible region is in the first quadrant with the vertices (30,10), (90,10), (20,50), and (70,30).

The minimum value of C is (Fill in the blank)____ and occurs when x = (Fill in the blank)____ and y = (Fill in the blank)____

Practice Problem #4

Minimize the objective function: R = 6x + 20y

The graph of the feasible region is shown.

HintRemember, find the vertices of the feasible region and plug it into R. The smallest value you can get for R is the minimum value, and the x and y you plugged in are the other answers.

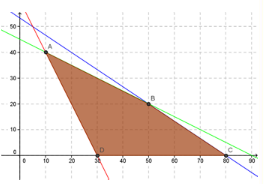
A coordinate plane with a system of inequalities graphed. The feasible region is in the first quadrant with the vertices (30,0), (60,0), (50,20), and (10,40).

The minimum value of R is (Fill in the blank)____ and occurs when x = (Fill in the blank)____ and y = (Fill in the blank)____