Introduction
Use the sliders in GeoGebra: Graphing Lines with the Same Slope to graph
- y = 2x + 8
- y = 2x − 4
- y = 2x + 1
- y = 2x − 7
To graph these lines in GeoGebra, you will need to do the following:
- Move the first slider so that the slope = 2.
- Change each of the following sliders to the correct y-intercept of each line.
Question #1 - Complete this sentence: Lines with equal slopes form a set of _____ (Fill in the blank) lines.
Now, use GeoGebra to graph:
- y = −3x + 8
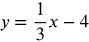
Now, graph
- y = 6x + 1
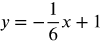
Question #2 - How are the slopes related in each of the above pairs of equations?
Question #3 - What type of lines are formed in this situation? If you need more graphs to determine the answers to the above questions use these:
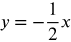
- y + 2x + 3
- y = −x − 5
- y = x + 2
Now, answer these questions:
- Complete this sentence: Lines with equal slopes form a set of _________ (Fill in the blank) lines.
- How are the slopes related in each of the Graph Set 2 equations?
- What types of lines are formed in the Graph Set 2 equations?
Following successful completion of this lesson, students will be able to...
- Create equations in two or more variables to represent relationships between quantities.
Enduring Understandings
- You can solve real-world problems using equations and inequalities.
- Operations create relationships between numbers.
- The language of mathematics is communicated through specialized vocabulary and symbols used to represent and describe mathematical ideas, generalizations, and relationships.
- By describing patterns using mathematics, we can make predictions and generalizations, analyze situations in everyday life, and sort and classify things.
The above objectives correspond with the Alabama Course of Study: Algebra II with Statistics standards: 8, 13, and 16.