Try It

Graphing Step Functions Practice Problems

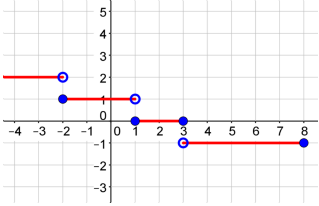
Practice Problem #1

Graph the step function. Pay close attention to your endpoints.

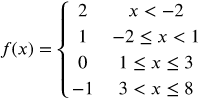
f of x equals 4 cases Case-: 1 2 x is less than negative 2 Case-: 2 1 negative 2 is less than or equal to x is less than 1 Case-: 3 0 1 is less than or equal to x is less than or equal to 3 Case-: 4 negative 1 3 is less than x is less than or equal to 8

Graph the first piece of the function.

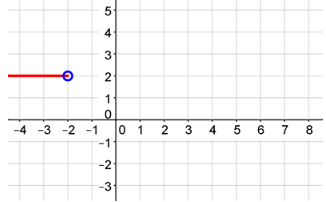
A horizontal ray at y = 2 graphed on a coordinate plane that goes left forever with an open endpoint at (negative 2, 2).

Graph the second piece of the function.

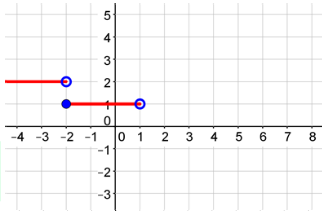
Going left to right, the first graph is a horizontal ray at y = 2 that goes left forever with an open endpoint at (negative 2, 2). The second graph is a horizontal segment at y = 1 that starts with a closed endpoint at (negative 2, 1) and ends with an open endpoint at (1,1).

Graph the third piece of the function.

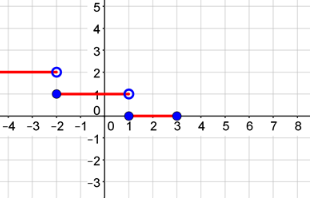
Going left to right, the first graph is a horizontal ray at y = 2 that goes left forever with an open endpoint at (negative 2, 2). The second graph is a horizontal segment at y = 1 that starts with a closed endpoint at (negative 2, 1) and ends with an open endpoint at (1,1). The third graph is a horizontal segment at y = 0 that starts with a closed endpoint at (1,0) and ends with a closed endpoint at (3,0).

Graph the fourth piece of the function.

Going left to right, the first graph is a horizontal ray at y = 2 that goes left forever with an open endpoint at (negative 2, 2). The second graph is a horizontal segment at y = 1 that starts with a closed endpoint at (negative 2, 1) and ends with an open endpoint at (1,1). The third graph is a horizontal segment at y = 0 that starts with a closed endpoint at (1,0) and ends with a closed endpoint at (3,0). The fourth graph is a horizontal segment at y = negative 1 that starts with an open endpoint at (3, negative 1) and ends with a closed endpoint at (8, negative 1).

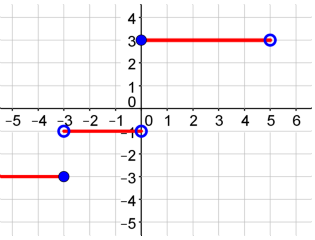
Practice Problem #2

Graph the step function below. Pay close attention to your endpoints.

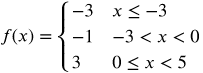
f of x equals 3 cases Case-: 1 negative 3 x is less than or equal to negative 3 Case-: 2 negative 1 negative 3 is less than x is less than 0 Case-: 3 3 0 is less than or equal to x is less than 5

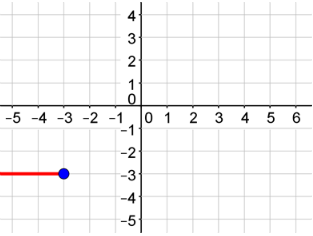
Graph the first piece of the function.

A horizontal ray at y = negative 3 graphed on a coordinate plane that goes left forever with a closed endpoint at (negative 3, negative 3).

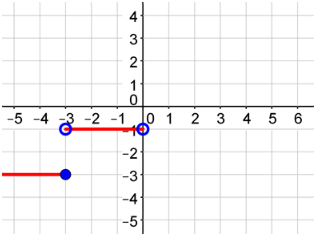
Graph the second piece of the function.

Going left to right, the first graph is a horizontal ray at y = negative 3 graphed on a coordinate plane that goes left forever with a closed endpoint at (negative 3, negative 3). The second graph is a horizontal segment at y = negative 1 that starts with an open endpoint at (negative 3, negative 1) and ends with an open endpoint at (zero, negative 1).

Graph the third piece of the function.

Going left to right, the first graph is a horizontal ray at y = negative 3 graphed on a coordinate plane that goes left forever with a closed endpoint at (negative 3, negative 3). The second graph is a horizontal segment at y = negative 1 that starts with an open endpoint at (negative 3, negative 1) and ends with an open endpoint at (zero, negative 1). The third graph is a horizontal segment at y = 3 that starts with a closed endpoint at (0,3) and ends with an open endpoint at (5,3).

Practice Problem #3

You've been asked to graph this function:

y = { x − 2 − 3 ≤ x ≤ 0 2 x + 3 0 < x < 4 − x 4 ≤ x

You want to start by graphing the y = x − 2 piece. Which of the following T tables or x | y tables would be most helpful with graphing this piece?

a.

x y
-3  
-1  
0  

b.

x y
-3  
0  
4  

c.

x y
0  
1  
4  

d.

x y
4  
5  
6