Learn

What is a Step Function?

A step function is exactly as it sounds – a series of steps or stairs. This function is a piecewise function consisting of only horizontal lines, or constants.

Horizontal lines are written in the form y = k or f(x) = k where k is a constant. For example, y = 4 and f(x) = −2 are two examples of constant functions.

In the chart below you can see that the cost of shipping is dependent on the weight of the package.

Cost Weight (in lbs)
$7.50 0 < weight ≤ 5
$12.00 5 < weight ≤ 10
$20.50 10 < weight ≤ 20

You can easily graph this information as a function because it can be algebraically represented as the following function.

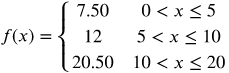
f of x equals 3 cases Case-: 1 7.50 0 is less than x is less than or equal to 5 Case-: 2 12 5 is less than x is less than or equal to 10 Case-: 3 20.50 10 is less than x is less than or equal to 20

 

Graphical Representation

You can create a graphical representation using the information.

After you graph each piece of the graph, you will have something that looks like the graph below.

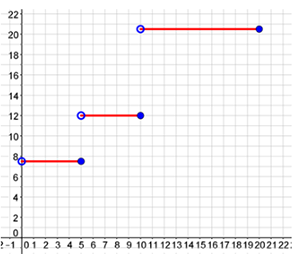
A step function graph with 3 horizontal segments. Going left to right, the first horizontal segment is at y = 7.5 that starts with an open endpoint at (0,7.5) and ends with a closed endpoint at (5,7.5). The second horizontal segment is at y = 12 that starts with an open endpoint at (5,12) and ends with a closed endpoint at (10,12). The third horizontal segment is at y = 20.50 that starts with an open endpoint at (10,20.5) and ends with a closed endpoint at (20,20.5).

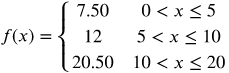
f of x equals 3 cases Case-: 1 7.50 0 is less than x is less than or equal to 5 Case-: 2 12 5 is less than x is less than or equal to 10 Case-: 3 20.50 10 is less than x is less than or equal to 20

From this graph, you can see that it looks like a staircase. Which interval is the largest with regard to weight?

  • 0 < x ≤ 5
  • 5 < x ≤ 10
  • 10 < x ≤ 20

On the graph, you notice there are several open points. These open points represent where you have only greater than instead of "or equal to" in your interval.

Example #1

Remember the word constraints? Some graphs that have contraints are called piece-wise graphs. They are "pieced" together. like the following example. The condition on these graphs is the domain beside each equation. The equation can only be graphed on the interval of the given domain.

Watch Graph Piecewise-Defined Functions.

Open Graph Piecewise-Defined Functions in a new tab

Note: The presentation may take a moment to load.

Example #2

Watch Graph Step Functions

Open Graph Step Functions in a new tab

Note: The presentation may take a moment to load.

Example #3

Watch Graph Step Functions

Open Graph Step Functions in a new tab

Note: The presentation may take a moment to load.

Do You Always Have a Line Segment?

Sometimes step functions include intervals that extend to infinity or negative infinity. This means the graph will have one or more rays as part of the graph.

Note: On some graphing calculators or apps, the arrows may not show on the screen, but know that the far left and far right parts of the graph extend indefinitely.

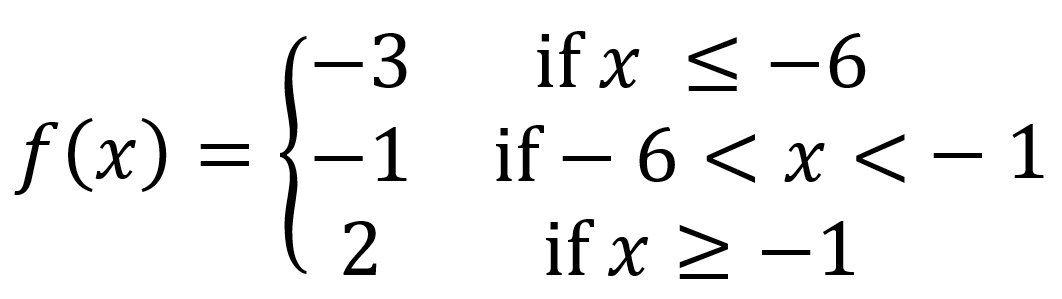
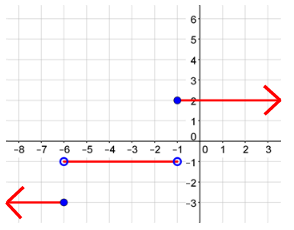
the peicewise function f of x is equal to negative 3 if x is less than or equal to negative 6, negative1 if x is greater than negative 6 and less than negative 1, 2 if x is greater than or equal to negative 1.A step function graph with 2 horizontal rays and 1 horizontal segment. Going left to right, the first graph is a horizontal ray at y = negative 3. The horizontal ray goes left forever and has a closed endpoint at (negative 6, negative 3). The second graph is a horizontal segment at y = negative 1 that starts with an open endpoint at (negative 6, negative 1) and ends with an open endpoint at (negative 1, negative 1). The third graph is a horizontal ray at y = 2. The horizontal ray goes right forever with a closed endpoint at (negative 1, 2).

 

Example #4

Watch Graph Step Functuions

Open Graph Step Functions in a new tab

Note: The presentation may take a moment to load.