Try It
Scatter Plots Practice
Practice Problem #1
A correlation is a measure of the strength of a relationship between two quantities. In your notebook, plot each ordered pair on a graph to make a scatter plot. Then determine the correlation.
Plot each ordered pair.
- (10, 1)
- (7, 0)
- (5, −2)
- (4, −4)
- (1, −6)
- (0, −7)
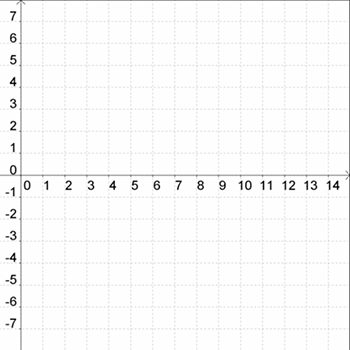
Answer:
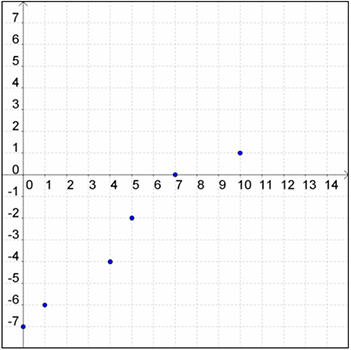
Is this a positive or negative correlation?
Answer: Positive
Practice Problem #2
Make a scatterplot of the data in the table and determine the relationship.
| Dollars Spent | Gallons Bought |
|---|---|
| 10 | 2.5 |
| 11 | 2.8 |
| 9 | 2.3 |
| 10 | 2.6 |
| 13 | 3.3 |
| 5 | 1.3 |
| 8 | 2.2 |
| 4 | 1.1 |
Answer:
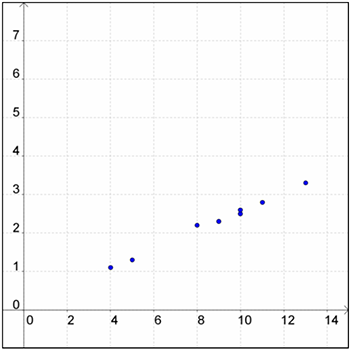
What type of relationship does the scatter plot show? Positive or negative?
Answer: Positive
Why do you believe the data in this case is scattered and not linear (a completely straight line)?
Answer: All of the points do not appear on a straight line, so it's not linear. The reason it's not linear is because the gas prices tend to fluctuate or change.
Practice Problem #3
Match each graph to the correct correlation.
Graphs:
Correlations:
- Positive
- Negative
- No Trend
Answers:
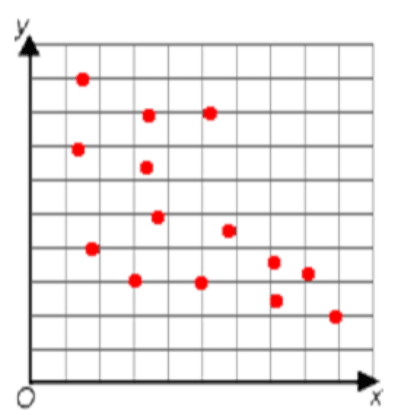
Negative
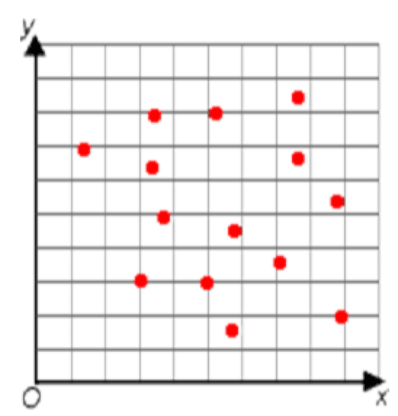
No Trend
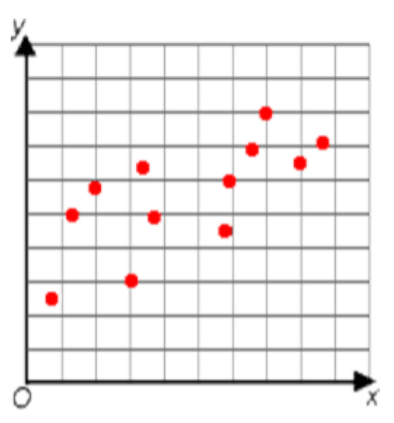
Positive
Line of Best Fit Practice
Practice Problem #4
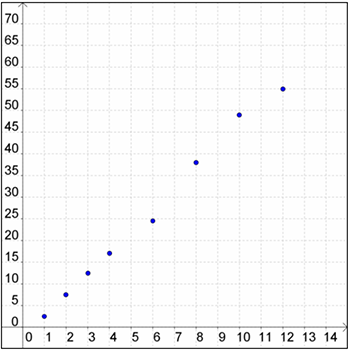
Use the data from the chart and plot the points. Draw the best fitting line and then compute the linear equation for that best fitting line.
| Age (months) | Weight (lbs) |
|---|---|
| 1 | 2.5 |
| 2 | 7.5 |
| 3 | 12.5 |
| 4 | 17 |
| 6 | 24.5 |
| 8 | 38 |
| 10 | 49 |
| 12 | 55 |
First, plot the points and check the answer.
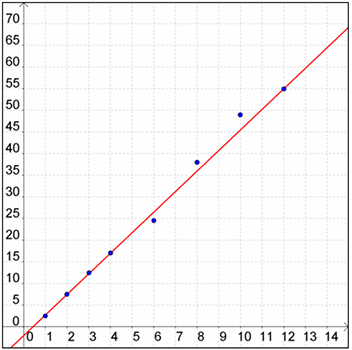
Next, draw a line that best fits the data and check the answer.
Now, we need to compute the linear equation for that best fitting line. Choose two points that fall on the line that you have drawn. Let's use (4, 17) and (12, 55). Use the formula to find the slope.
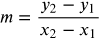
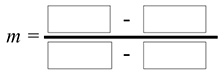
- Enter the coordinate numbers into the formula.
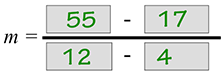
- Simplify.
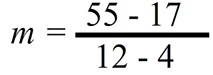
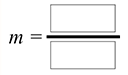
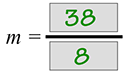
- Simplify again.
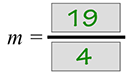
Next, find the y-intercept using slope-intercept form and one of the points. Let's use (4, 17).
- y = mx + b
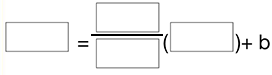
- Substitute the slope and coordinates into the slope-intercept equation.
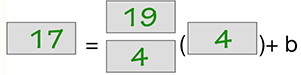
- Simplify.
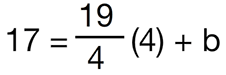
- 17 = 19 + b
- ___blank = b
- −2 = b
Finally, plug the slope and y-intercept into the slope-intercept form to get the linear equation for this line.
- y = mx + b
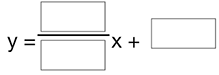
- Substitute the slope and intercept into the slope-intercept equation.
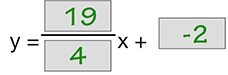
- The equation for our line is:
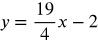
You've completed these review activities!