Learn
Sequences
Remember to think about the following question, so that you can answer it at the end of the lesson.
How are the problems in the Introduction section similar to the examples in this Learn section?
Arithmetic sequences can be used to model real-world events. In this lesson, you will learn how to find the missing parts of an arithmetic sequence.
Arithmetic Sequence
An arithmetic sequence is a sequence in which the difference between each term and the preceding term is always constant. It is sometimes called an arithmetic progression.
We see these type of patterns in certain flower beds. They use these patterns to make them look presentable.

Example #1
Open Determine if a Sequence is an Arithmetic Sequence Example #1 in a new tab
Example #2
Open Determine if a Sequence is an Arithmetic Sequence Example #2 in a new tab
Example #3
We can also identify if an arithmetic sequence is a function. Consider the number sequence 1, 5, 9, 13, 17.... We will simply pair up the sequence number with the value.
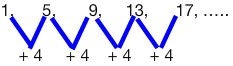
The common difference is 4, therefore it is an arithmetic sequence. By pairing the sequence number with the value, we produce the following pairs:
(Sequence #, Value in that sequence)
(1,1), (2,5), (3,9), (4,13), (5,17)
Are these pairs of numbers a function?
Example #4
Let's look at another sequence and determine if it is a function. Consider the number sequence: 5, 3, 1, −1, −3, ....
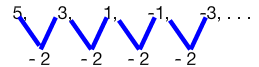
The common difference is −2, therefore it is arithmetic. This produces the following pairs:
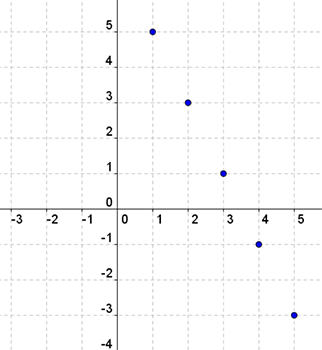
(1,5), (2,3), (3,1), (4,−1), (5,−3)
Look at the graph of the coordinate points. Check to see if these numbers are a function. Do they pass the vertical line test?
Geometric Sequence
In the arithmetic part of the lesson, you have studied a sequence that has a common difference (arithmetic). We are going to study another type of sequence called a geometric sequence. Instead of having a common difference, it has a common ratio. The ratio is what you multiply each number by to get the next term.
A sequence in which the ratio between consecutive terms is constant is called a geometric sequence.
Anytime we borrow money and pay interest we experience a geometric sequence.
- To find the ratio, divide any term following the first term by the preceding term.
- To find the next term in a sequence, multiply the given term by the common ratio.
Example #5
Open Determine if a Sequence is a Geometric Sequence Example #5 in a new tab
Example #6
Open Determine if a Sequence is a Geometric Sequence Example #6 in a new tab
Example #7
We can determine if geometric sequences are functions the same way we did arithmetic. Take these pairs of numbers and check to see if it is a function.
We simply make pairs with the sequence number and the value from the video Determine if a Sequence is a Geometric Sequence Example #5 to see if x-value repeats and is paired with exactly one y-value.
Example: (1,2), (2,10), (3,50), (4,250)
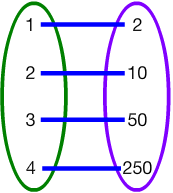
Looking at the mapping of the values, is it a function?