Learn

Types of Functions

The Graph of a Linear Function

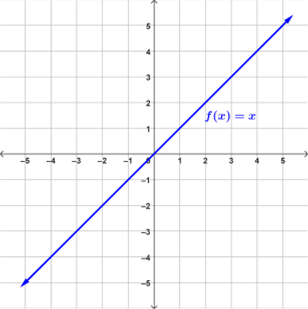
This is what the graph of a linear function would look like. The term linear means "line". The basic equation for a linear function is f (x) = x. When the linear function, f (x) = x, is graphed on a coordinate plane, it is a straight line that passes through the origin and has a slope of 1.

The graph of f (x) = x is shown.

Slope-Intercept Form of Linear Function

The slope of a linear function is the measure of the steepness of its graph. The y-intercept of a linear function is the point where its graph crosses the y-axis on a coordinate plane. The slope-intercept form of the equation of a linear function is f(x) = mx + b, where m is the slope of its graph and b is the y-coordinate of the y-intercept. For example, the function, f(x) = 3x – 1, has a slope of 3 and a y-intercept of (0,–1).

Examples of Linear Functions

Below are examples of graphs of linear functions.

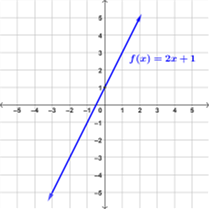
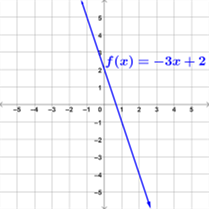
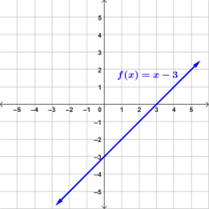
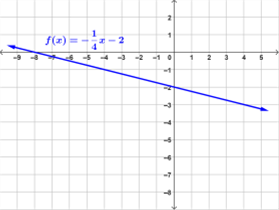
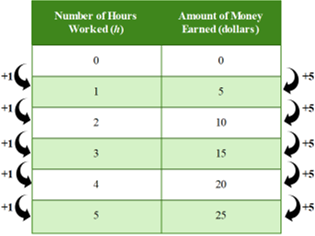
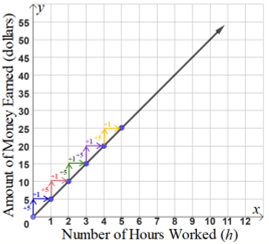
Linear Functions in Real Life Situations

There are lots of real life cause and effect situations that can be represented by a linear function. For example, you have a job that pays $5 per hour. There is a linear relationship between the number of hours you work and the amount of money you earn. As the number of hours worked goes up by 1, the amount of money earned goes up by $5 dollars.

The given situation represents a straight line when graphed on a coordinate plane.

Quadratic Function

There are also other types of functions that represent cause and effect. If you throw something up, it must come down. This would be considered a quadratic function or better known as a parabola.

If you shoot drops of water upwards, they fall back to earth in an arc, like a parabola.
The dish of a TV satellite is a parabola.

Basic Equation and Graph of a Quadratic Function

The basic equation for a quadratic function is f (x) = x2. All quadratic functions have the shape of a parabola. Parabolas have a “U” shape. The graph of f (x) = x2 is shown.

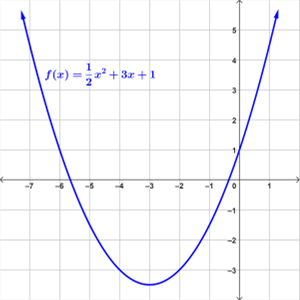
Standard Form of a Quadratic Function

The standard form of the equation of a quadratic function is f(x) = ax2 + bx + c, when a, b, and c are all real numbers.

Below are two examples of graphs of quadratic functions.

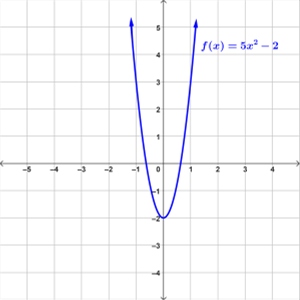
Exponential Function

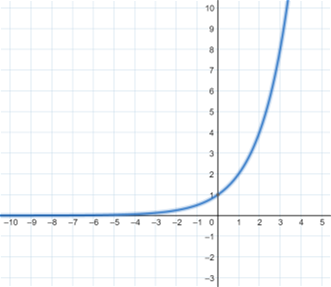
An exponential function is best described as a snowball. The snowball gets bigger and bigger as it rolls down the mountain. The basic equation for an exponential function is f (x) = bx, where b is any positive number not equal to one. The graph of f (x) = 2x is shown.

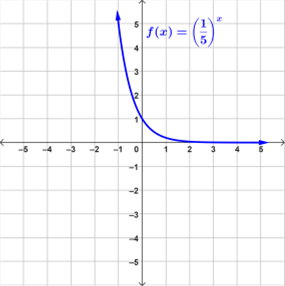
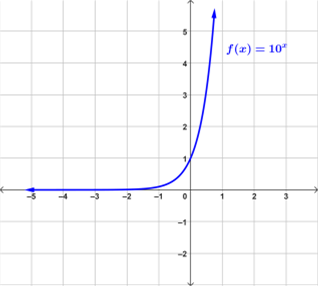
Examples of Exponential Functions

Below are examples of graphs of exponential functions.

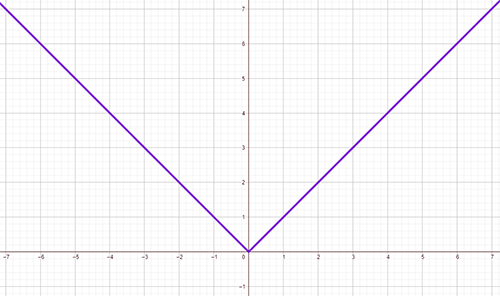
Absolute Value Function

Absolute value functions have a V shape and have a similar number pattern to a parabola.

The basic equation for an absolute function is: f(x) = |x|

The graph of f(x) = |x| is shown.

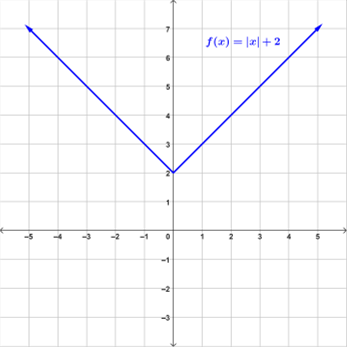
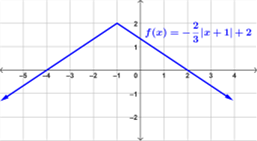
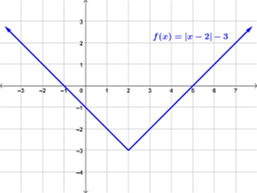
Graph of the absolute function f of x equals absolute value of x. The V-shaped graph decreases from the left passing through points (negative 6, 6), (negative 5, 5), (negative 4, 4), (negative 3,3), (negative 2,2), (negative 1,1) and (0,0) then increases as it passes through points (1,1), (2,2), (3,3), (4,4), (5,5), and (6,6).
See larger version of an absolute value function graph here.

Examples of Absolute Value Functions

Below are examples of graphs of absolute value functions.

Polynomial Function

A polynomial function is any function that has an exponent of 2 or more. The following is an example of a polynomial function with an exponent of 3 in it: f(x) = x3 + 2x2 − x − 2

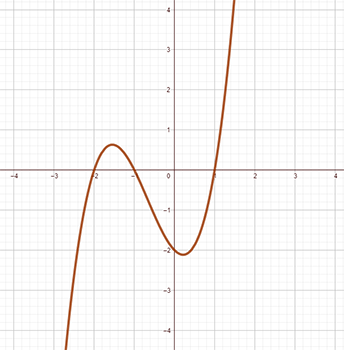
Polynomial function graph of the function f of x equals x cubed plus 2 x squared minus x minus 2. The graph contains two curves. Graph starts in the lower left and moves upwards through the points (negative 4, negative 30), (negative 3, negative 8), (negative 2, 0), and crosses the y axis. Then, it curves downwards and crosses the y axis through the points (negative 1, 0) and (0, negative 2). Next, it curves upwards again passing through the points (1, 0), (2, 12), (3, 40), and (4, 90).
See larger version of a polynomial graph of the function f(x) = x3 + 2x2 − x − 2 here.

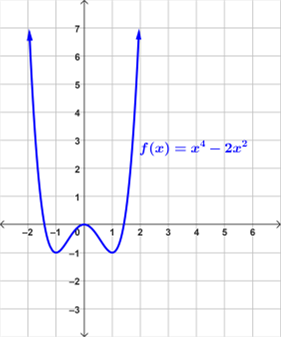
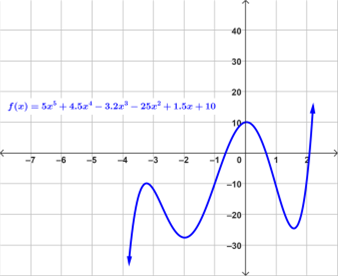
Examples of Polynomial Functions

Below are examples of graphs of polynomial functions.

Piecewise Function

A piecewise function is a function that is made up of two or more different functions (pieces) throughout its domain. The following is a piecewise function that consists of two linear pieces.

The first piece represents the function, f(x) = x + 1, from x values of 0 to 2.

The second piece represents the function, f(x) = ½x + 3, from x values of 2 to 4.

The piecewise function can be written as

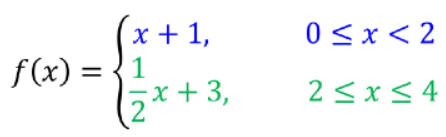
Another Piecewise Function

Below is the graph of a piecewise function.

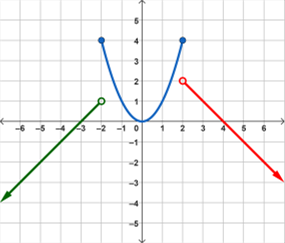
The function is written as:

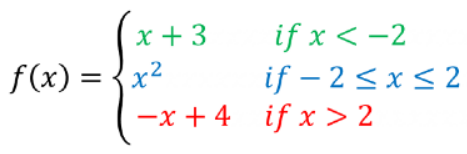
Step Functions

Step functionsliterally look like steps. An example of what step functions represent would be having to pay a different price for something depending upon the weight.

For example: If a letter weighs between 1-2 ounces then it will cost 41 cents, but the cost goes up after it increases past 2 ounces.