Try It
Understanding Functions Practice
Practice Problem #1
Given the relation {(−5, 3), (4, 7), (−2, −3), (6, 7)}, determine the domain, range, and whether the relation is a function.
What is the domain of the relation?
- −3, 3, 7
- −5, −2, 4, 6
- −5, 3, 4, 7, −2, −3, 6, 7
Answer: b. −5, −2, 4, 6. The domain is the first number in each pair listed in order from least to greatest.
What is the range of the relation?
- −3, 3, 7
- −5, −2, 4, 6
- −5, 3, 4, 7, −2, −3, 6, 7
Answer: a. −3, 3, 7. The range is the second number in each pair of numbers, also listed in order from least to greatest. Remember to not write repeated values.
Is this relation a function?
- Yes
- No
Answer: a. Yes. This relation is a function because each x-value (domain value) corresponds to one and ony one y-value (range value).
Practice Problem #2
Given the relation {(0, −1), (−5, 4), (−1, 6), (0, 12), (1, −1)}, determine the domain, range, and whether the relation is a function.
What is the domain of the relation?
- −1, 1, 4, 0, 12
- −1, 0, 4, 6, 12
- −5, −1, 0, 1
Answer: c. −5, −1, 0, 1. The domain is the first number in each pair of coordinates, also called x-values. Write numbers in order from least to greatest and do not repeat any numbers.
What is the range of the relation?
- −1, 1, 4, 0, 12
- −1, 4, 6, 12
- −5, −1, 0, 1
Answer: b. −1, 4, 6, 12. The range of the function is the second value in each pair of numbers. Remember to not write repeated values and write your values in order from least to greatest.
Is this relation a function?
- Yes
- No
Answer: b. No. The correct answer is no because you have repeated x-values (or domain values). For the relation to be a function, you cannot have an x-value that corresponds to more than one y-value.
Practice Problem #3
Determine if the mapping is a function.
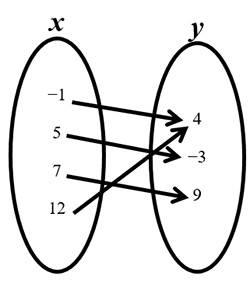
Is this mapping a function?
- Yes
- No
Answer: a. Yes. This is a function because none of the domains are used more than once.
Practice Problem #4
Given the relation below, draw a mapping to represent the relation. Then determine if it represents a function.
Relation: (−2, 5), (0, 3.5), (2, 5), (5, 0)
Domain
- −2
- 0
- 2
- 5
Range
- 0
- 3.5
- 5
Map the relation.
Answer:
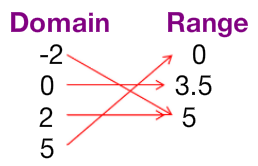
Is this a function?
- Yes
- No
Answer: a. Yes. This is a function, as none of the domains are used more than once.
Practice Problem #5
Given the relation below, draw a mapping to represent the relation. Then determine if it represents a function.
Relation: (−4, 2.1), (3, 10), (0, 2.1), (−4, 5)
Domain
- −4
- 0
- 3
Range
- 2.1
- 5
- 10
Map the relation.
Answer:
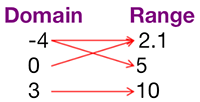
Is this a function?
- Yes
- No
Answer: b. No. This is not a function, as one of the domains (−4) is used more than once.
Practice Problem #6
Use the vertical line test to determine whether or not the following relation is a function.
Relation: (4, 2), (4, −2), (0, 0), (1, 1), (1, −1)
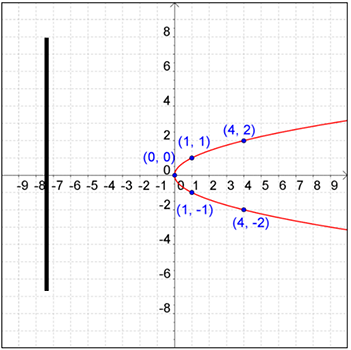
Is this a function?
- Yes
- No
Answer: b. No. This is not a function. The vertical line crosses the relation in more than one location.
Practice Problem #7
Determine if the graph is a function.
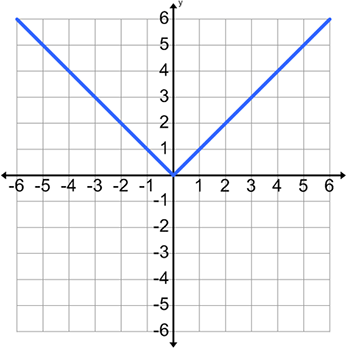
Is this graph a function?
- Yes
- No
Answer: a. Yes. The graph is considered a function because it passes the vertical line test.
Practice Problem #8
Determine if the graph is a function.
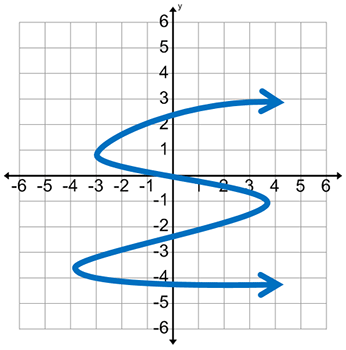
Is this graph a function?
- Yes
- No
Answer: b. No. The graph is not a function because it fails the vertical line test.
Practice Problem #9
Determine if the graph is a function.
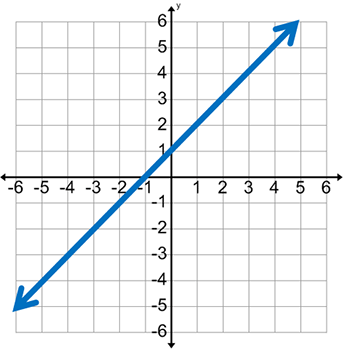
Is this graph a function?
- Yes
- No
Answer: a. Yes. The graph is considered a function because it passes the vertical line test.
You've completed this review activity!