Learn
Relations
In mathematics, a relation is simply a set of ordered pairs within a set. The symbols { and } are used to denote a relation.
In fact, any two things can be a relation, as long as it comes in a pair. For instance, suppose there were three pairs of twins in a room. This would be an example of a relation because they came in pairs.
Some examples of relations are below:
- {(3, 5), (4, −7), (−9, 2), (0, −5)}
- {(−1, 9), (−15, −3), (8, −1), (4, −4)}
- {(blue, green), (red, white), (pink, yellow)}
- {(x, y), (m, a), (z, n), (t, c)}
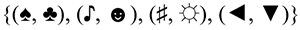
Even the last example is a relation because the symbols are grouped in pairs.
Domain and Ranges
In a relation, there are two numbers or objects in pairs. With each pair, the first number or object is called the domain. The second number in each pair is called the range.
Example #1
Given the relation {(−1, 9), (−15, −3), (8, −1), (4, −4)}, determine the domain and range of the relation.
- Domain: −1, −15, 8, 4
- Range: 9, −3, −1, −4
However, you will want to write these values in order from least to greatest. Therefore, the domain and range will be:
- Domain: −15, −1, 4, 8
- Range: −4, −3, −1, 9
Example #2
Given the relation {(−6, −3), {(2, −4), (6, 8), (−11, 2)}, determine the domain and range of the relation. Remember to write in order from least to greatest.
First, determine the domain:
- Domain: ___blank, ___blank, ___blank, ___blank
- Hint: What is the first value for each pair of numbers?
- Answer: Domain: −11, −6, 2, 6
Next, determine the range:
- Range: ___blank, ___blank, ___blank, ___blank
- Hint: What is the second value for each pair of numbers?
- Answer: Range: −4, −3, 2, 8
Functions
A function is a relation that pairs each x-value with exactly one y-value. This means that a relation is a function if the domain values do not repeat.
If you have the relation {(−2, 5), (3, −7), (4, 9)}, this is an example of a function because each x-value corresponds to only one y-value.
The x-value is the x-coordinate, often called the independent variable.
The y-value is the y-coordinate, often called the dependent variable. The y-value is dependent on x, which is why y is called the dependent variable.
Representing a Function
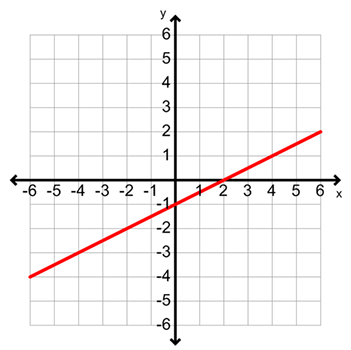
Functions can be represented in many ways: ordered pairs, equations, table of values, mapping diagrams, and graphs. Examples of these representations are shown below.
Ordered Pairs: {(0,1), (1,2), (2,4), (3,8)}
Equation: f(x) = 2x + 2
Table:
| x | y |
|---|---|
| −2 | 4 |
| −1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
Mapping:
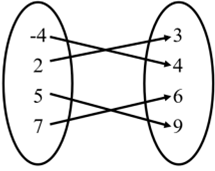
Graph:
Determine Whether a Given Relation is a Function
Open Determine Whether a Given Relation is a Function in a new tab
Example #3
Given the relation {(2, 4), {(4, 8), (5, 10), (7, 14)}, determine the domain and range of the relation. Also tell if it is a function. Justify your answer.
First, determine the domain:
- Domain: ___blank, ___blank, ___blank, ___blank
- Answer: Domain: 2, 4, 5, 7
Next, determine the range:
- Range: ___blank, ___blank, ___blank, ___blank
- Answer: Range: 4, 8, 10, 14
Next, determine whether the relation is a function:
Are there any repeating domain values? Answer: No.
Is the relation a function? Answer: Yes. The relation is a function because each x-value (domain value) is paired with only one y-value (range value).
Example #4
Given the relation {(–4, 5), {(–1, –3), (3, 5), (–1, 8)}, determine the domain and range of the relation. Also tell if it is a function. Justify your answer.
First, determine the domain. Write all repeated values once.
- Domain: ___blank, ___blank, ___blank
- Answer: Domain: −4, −1, 3
Next, determine the range. Write all repeated values once.
- Range: ___blank, ___blank, ___blank
- Answer: Range: −3, 5, 8
Next, determine whether the relation is a function:
Are there any repeating domain values? Answer: Yes. The x-value (domain value), −1, repeats. It is paired with two y-values (range values), −3 and 8.
Is the relation a function? Answer: No. The relation is not a function because the x-value (domain value), −1, is paired with two y-values (range values).
Determine if a Mapping is a Function
Open Determine if a Mapping is a Function in a new tab
Determine if a Table of Values is a Function
Open Determine if a Table of Values is a Function in a new tab
Vertical Line Test
You can use the vertical line test to determine if a graph is a function. If given a graph, draw a vertical line over anywhere over the graph. You will have one of two things occur:
- If the vertical line intersects the graph at only one point, the graph is a function.
- If the vertical line intersects the graph at more than one point, the graph is not a function.
Determine if a Graph is a Function
Watch the video below to learn how to apply the vertical line test.
Open Determine if a Graph is a Function in a new tab
Example #5
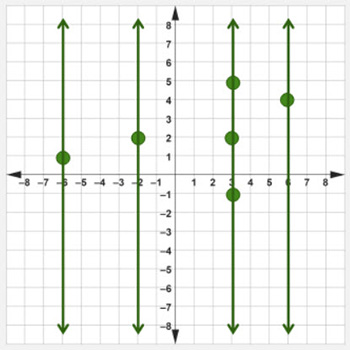
Use the vertical line test to determine if the given graph is a function. Justify your answer.
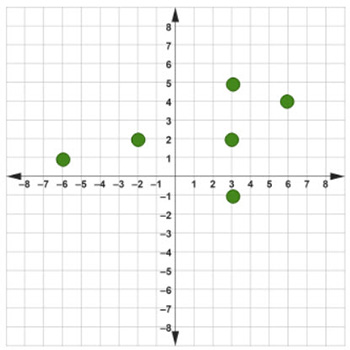
Step #1: Draw a vertical line through every point on the given graph.
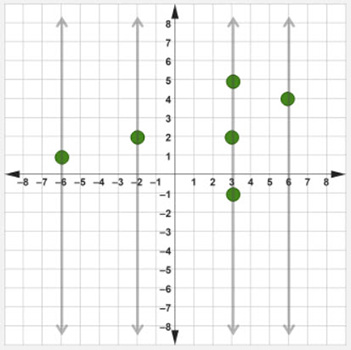
Step #2: Check to see if any of the vertical lines passes through two or more points on the given graph.
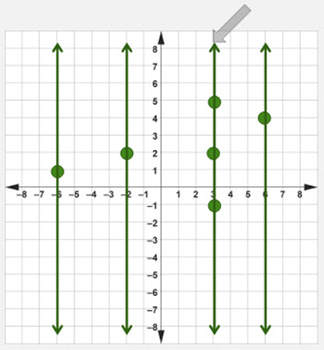
The third vertical line from the left passes through three points on the given graph.
Step #3: Determine if the given graph is a function.
The given graph is not a function.
Step #4: Justify your answer.

The given graph is not a function because there is a vertical line that passes through two or more points on it.
Example #6
Use the vertical line test to determine if the given graph is a function. Justify your answer.
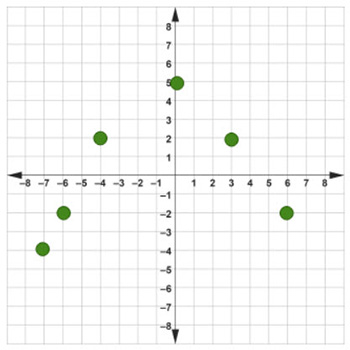
Step #1: Draw a vertical line through every point on the given graph.
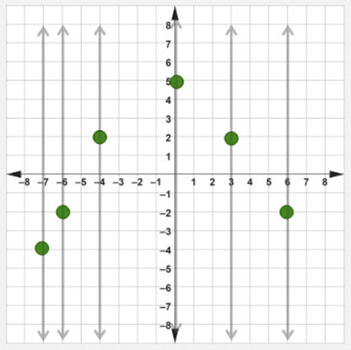
Step #2: Check to see if any of the vertical lines passes through two or more points on the given graph.
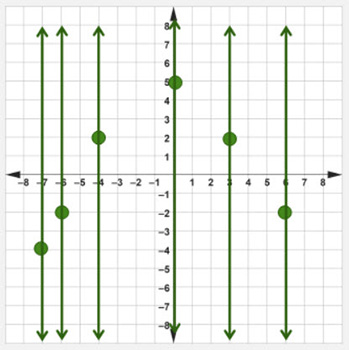
None of the vertical lines that were drawn in step 1 pass through two or more points on the given graph.
Step #3: Determine if the given graph is a function.

The given graph is a function.
Step #4: Justify your answer.

The given graph is a function because there is not a vertical line that passes through two or more points on the graph.